Сигналы, шумы и помехи. Автокорреляционная функция

Мы поговорим о сигналах, о том как их детектируют и проведем некую параллель с теми задачами, которые решаются на треке “Технологии беспроводной связи”.

Сигналы.

Есть полезные сигналы и есть шумы и помехи, которые являются мешающими.

Это все сигналы. Нужно уметь как-то поработать с шумами, научиться выделять их характерные особенности, а также понимать про те же самые особенности, которыми обладает наш полезный сигнал, который мы хотим передать. По сути дела, мы хотим сделать какую-то сортировку по какому-то параметру.

Биты и сигналы. Оцифровка.

Физическим элементом для передачи информации являются биты. Байты - удобные единицы для работы с информацией, но это просто наборы битов.

1 байт = 8 бит.

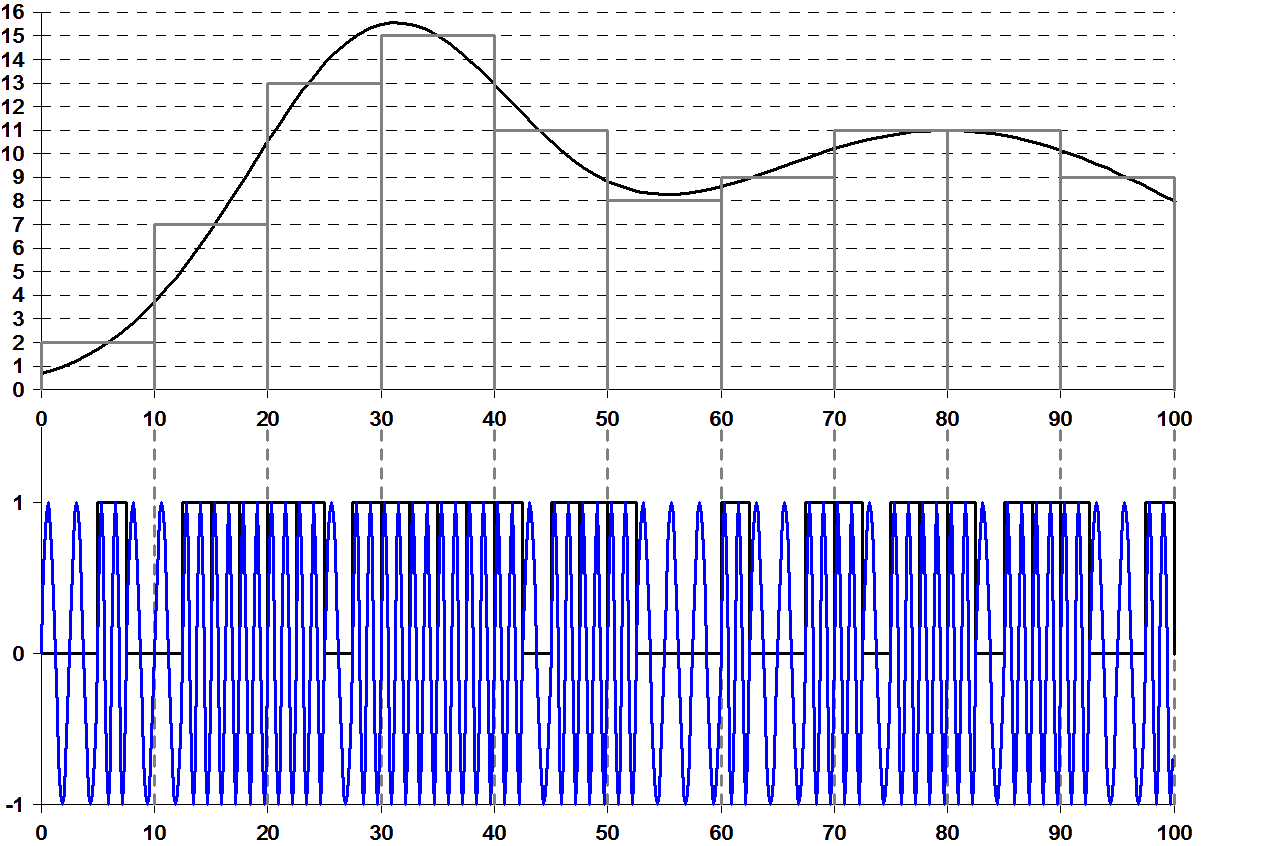
Биты представляют собой элементарные сигналы, которые излучаются, передаются, проходят через канал связи, претерпевает возможные искажения, на них налагаются шумы и только потом регистрируются. Остановимся на этой теме подробнее.

Сигналы на стенде ОВКС.

Вот пример последовательности сигналов, которые были получены на стенде с вращающимися шестеренками (ОВКС).

На видео вы видите, что шестеренки крутятся, в итоге регистрируется сигнал, что мы видим на временной оси.

Из вида стенда понятно, что шестерни имеют прорези, через которые инфракрасный сигнал проходит и регистрируется на фотодиоде. Когда фотодиод заслоняет стенка, соответственно сигнала нет, и вы видите некоторое запаздывание сигнала - это 0. Таким образом, фактически мы одной шестеренкой моделируем последовательность передачи бит по каналу связи.

На рисунке обозначен пример элементарного окошечка, который как раз играет роль вот этого самого бита - 1, и пример элементарной стеночки, которая играет роль - 0.

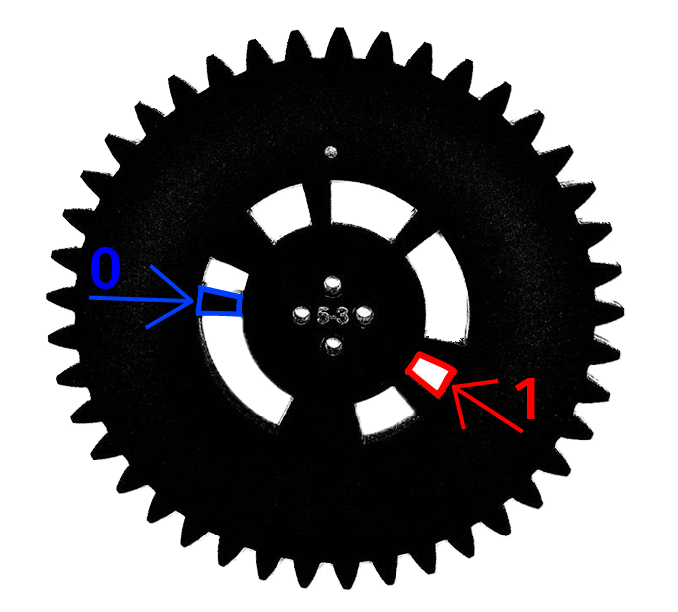
Фактически, шестеренка - это некоторая последовательность бит, которая передается. Последовательность сигналов, которая видна на графике, по сути дела, это тот сигнал, который пришёл к приемнику.

Обратите внимание, что сигнал не идеальный, то есть вы видите, что фронт сигнала не бесконечно малый - есть какое-то время, когда 0 сменяется 1. Кроме того, вроде бы шестеренку мы сделали очень хорошо, аккуратно, все грани одинаковые, но есть характерные особенности, которые видны невооруженным взглядом на фронтах. И эти фронты отличаются.

То есть, несмотря на то, что мы сделали всё аккуратно, шестерни вращаются с одной угловой скоростью, все-таки есть небольшие отличия в сигналах. Эти отличия вы можете здесь наблюдать, и такие же отличия существуют в реальных системах передачи данных. Не бывает полностью сигналов близнецов, они всегда немного отличаются.

Кроме того, вы можете видеть небольшие вариации амплитуды сигнала - это как раз шум. Это шум, связанный с тем, что вокруг нас есть источники шума. Они влияют и на ИК, работают в ИК диапазоне, также как работают в радиодиапазоне, и работают гигагерцовом диапазоне. Источники шумов есть в любом диапазоне частот, и вы видите присутствие данного шума. Таким образом, данная последовательность сигналов вам визуализирует, что фактически происходит передача данных.

Когда приемник принимает сигналы, ему нужно разобраться где же всё-таки 0, а где всё-таки 1? Поговорим немного об анализе сигналов, чтобы вы понимали, какие виды инструментов есть сейчас у нас в руках.

Давайте внимательно посмотрим на эти сигналы и подумаем, каким же образом в принципе можно было бы их детектировать. Один из способов такого детектирования - так называемый корреляционный приём. В чём заключается идея корреляционного приема (или когерентного приема)?

Корреляционный (когерентный) анализ. Автокорреляционная функция.

Его идея заключается в том, что вы знаете достаточно хорошо знаете, какой сигнал вы излучили, потому что в силу физических особенностей вы никогда не излучаете полную копию сигнала, которая была до этого. Они всё равно будут немного отличаться, но в целом они будут похожи, в среднем они одинаковые.

Таким образом, вы знаете модель сигнала - это очень интересная вещь. Например, в качестве сигнала мы рассматриваем эту последовательность импульсов, которые мы получили на нашей шестерне.

Задача, которую нам необходимо решить в треке, часто имеет отношение к детектированию сигналов и заключается в том, чтобы определить характерный период вращения шестерни вокруг своей оси. Чем шестерня вращается быстрее, тем большее количество импульсов на одном и том же временном интервале вы можете разглядеть.

А теперь давайте попробуем сделать автокорреляционную обработку, которая заключается в следующем: мы возьмем наш исходный сигнал и сдвинем его относительно себя, немножко совсем сдвинем. Посмотрите.

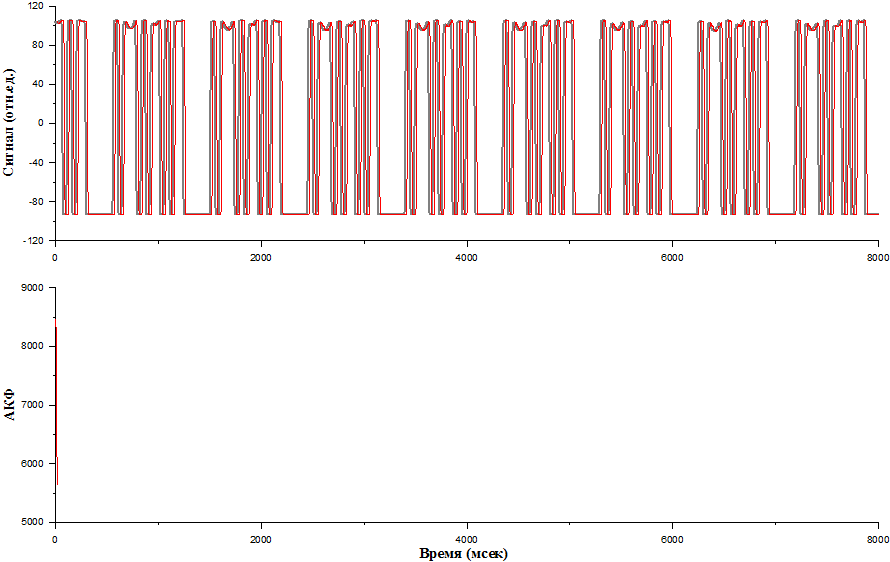
После этого перемножим эти две последовательности, то есть исходную и сдвинутую, приложим все отчёты в отчёты, и дальше все перемноженные отчёты просуммируем. Дальше сдвинем ещё на один временной отчет и опять всё просуммируем.

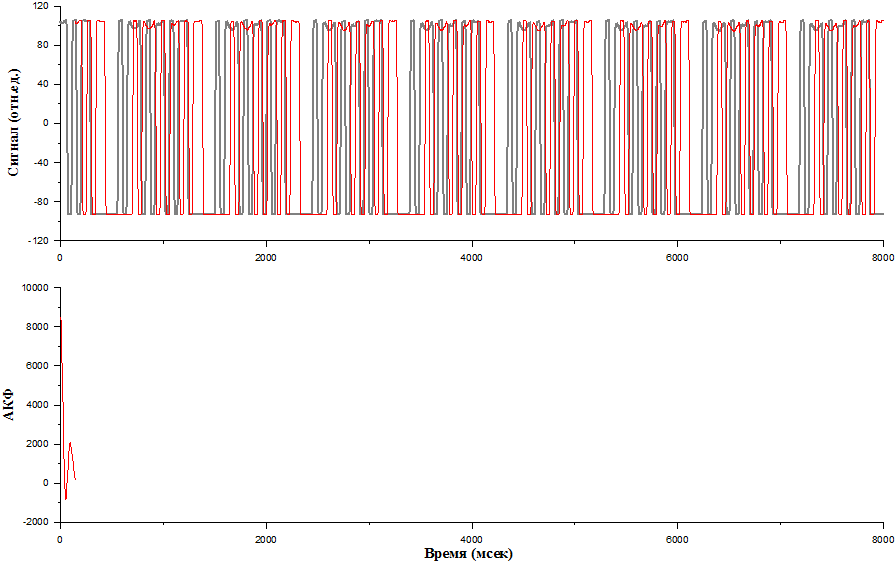
И так далее до тех пор, пока наши сигналы не разбегутся.

На данном графике вы видите, как выглядит так называемая автокорреляционная функция. Обратите внимание, что когда исходный сигнал не был сдвинут, то есть сдвижка равна нулю, то он по сути дела умножается сам на себя и суммируется, то мы видим пик.

Дальше, когда мы сдвигаем, амплитуда этой автокорреляционной функции немножечко уменьшается, сдвигаем дальше уменьшается еще больше.

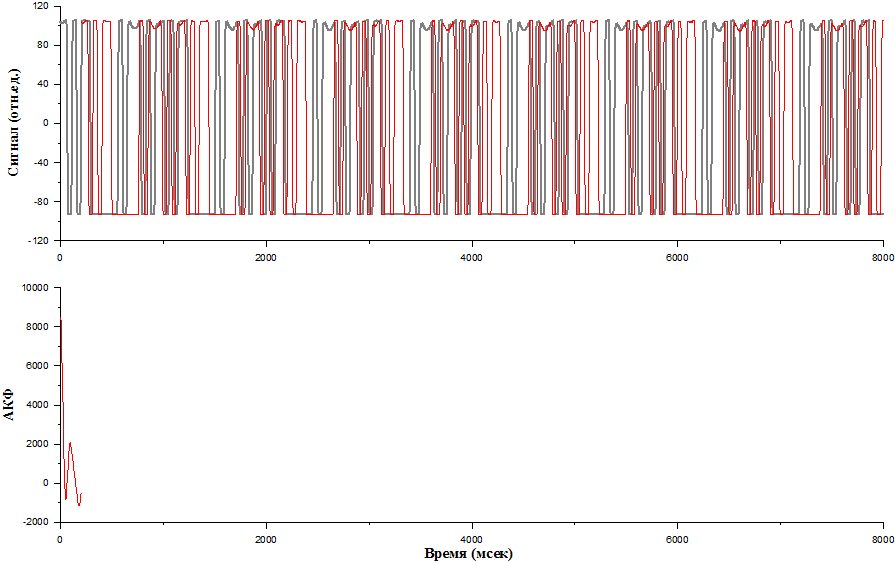
А дальше, интересно, она иногда становится отрицательной. Так бывает, то есть количество отчетов, которые не совпадают по знаку, оказалось больше, чем совпадающих.

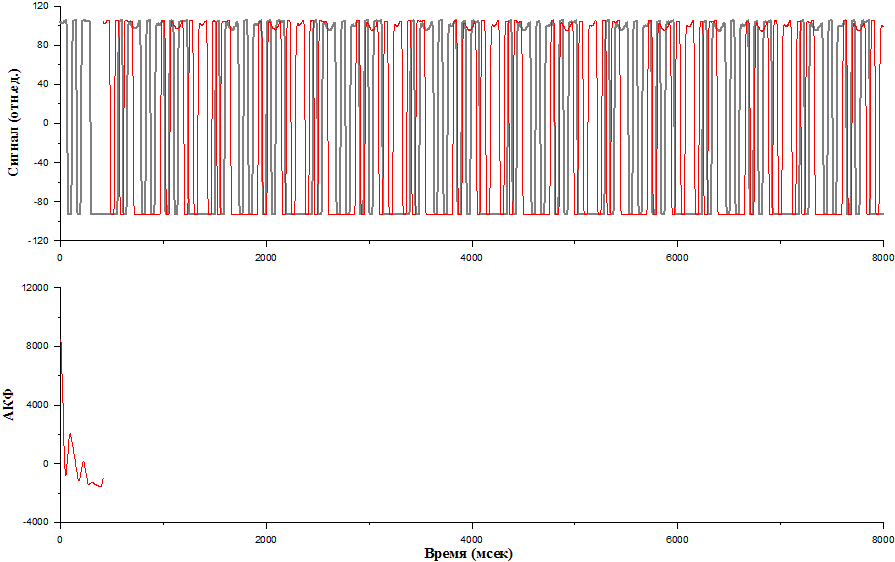
Дальше сдвигаем, сдвигаем, сдвигаем..

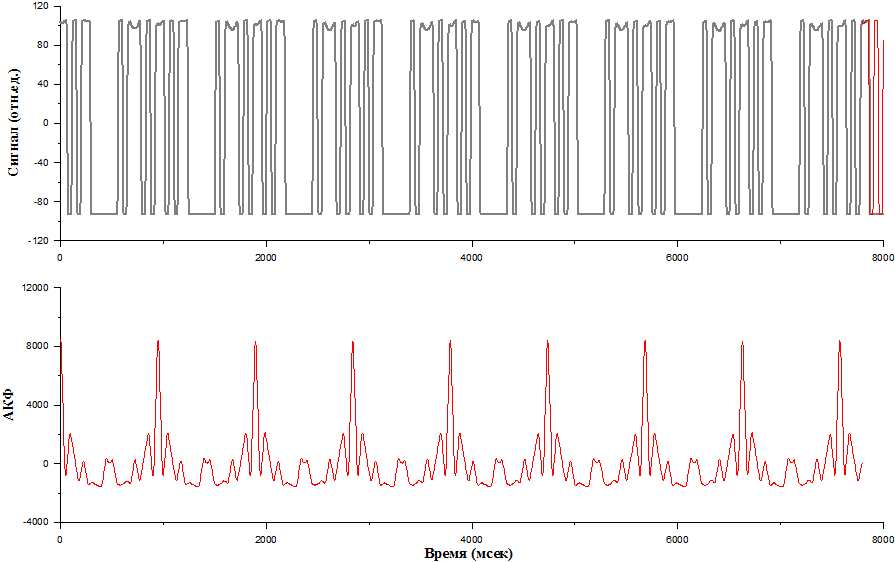
С каких-то пор, начиная с данного отчета, мы сдвинулись ровно на один период, и это привело к тому, что наши импульсы, сигналы опять совпали друг с другом, и вы опять видите пик.

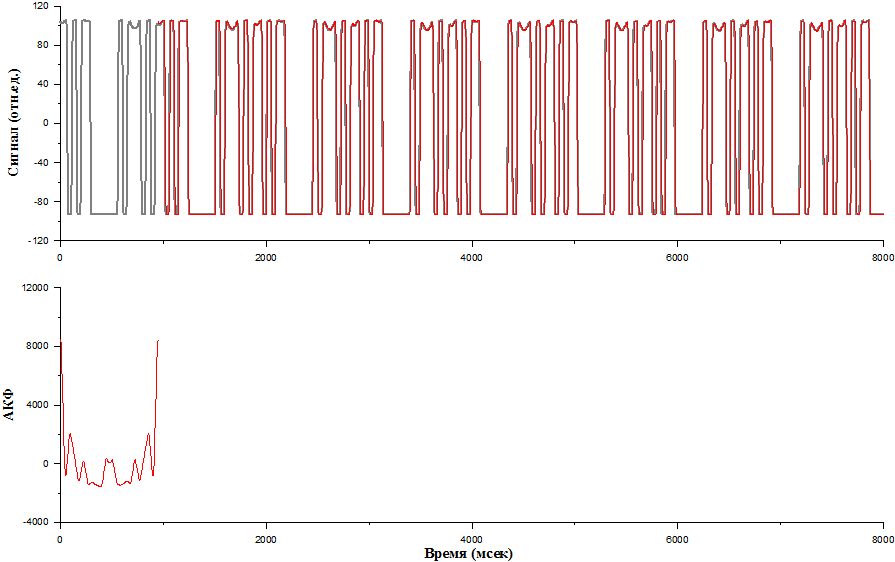
Повторяем процедуру до конца. В итоге вы видите последовательность пиков - это моменты времени, когда сигнал совпал сам с собой.

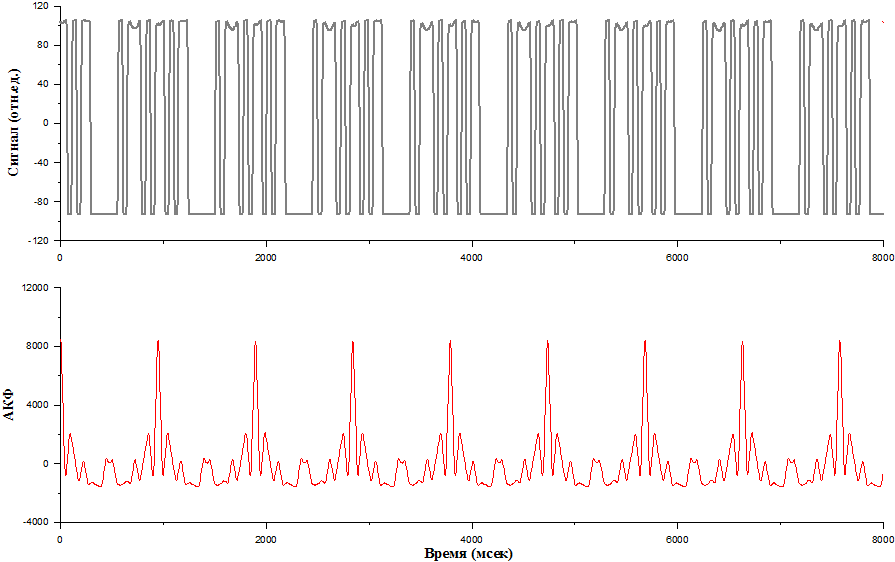
Теперь определить период вращения шестерни не представляет труда. Эти пики явно выражены, и основной пик называется основным лепестком автокорреляционной функции. Есть лепесточки, которые около 0 флуктуируют, это уже боковые лепестки автокорреляционной функции - 1-ый, 2-ой, 3-ий, и дальше опять вышли в основной лепесток автокорреляционной функцией.

То есть автокорреляционной анализ в данной конкретной задаче помогает определить скорость вращения шестерни, потому что в дальнейшем нам не составляет труда найти расстояние между всеми пиками, найти период вращения.

Итак, здесь явно выражен сигнал.

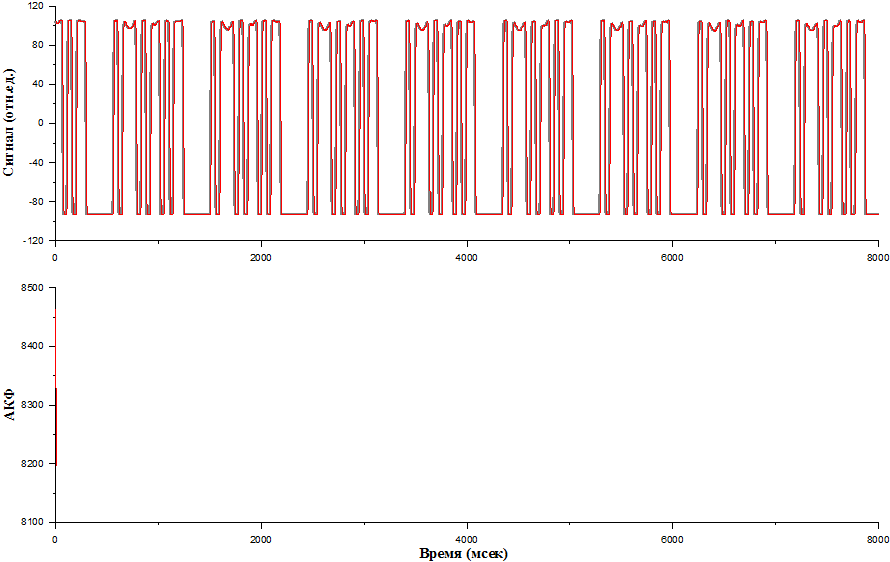
Теперь давайте сделаем следующее: возьмем из реализации уберём сигнал совсем, это означает, что мы взяли шестерню, у которой вообще нет окон. Давайте поставим эту шестерню, для полноты эксперимента её прокрутим, и получим сигнал. Обратите внимание, сигнал всё-таки какой-то есть. То есть нет такого, чтобы совсем-совсем-совсем 0-ли. Но он, конечно, намного слабее, и это шумы, которые непрерывно присутствует в нашем канале.

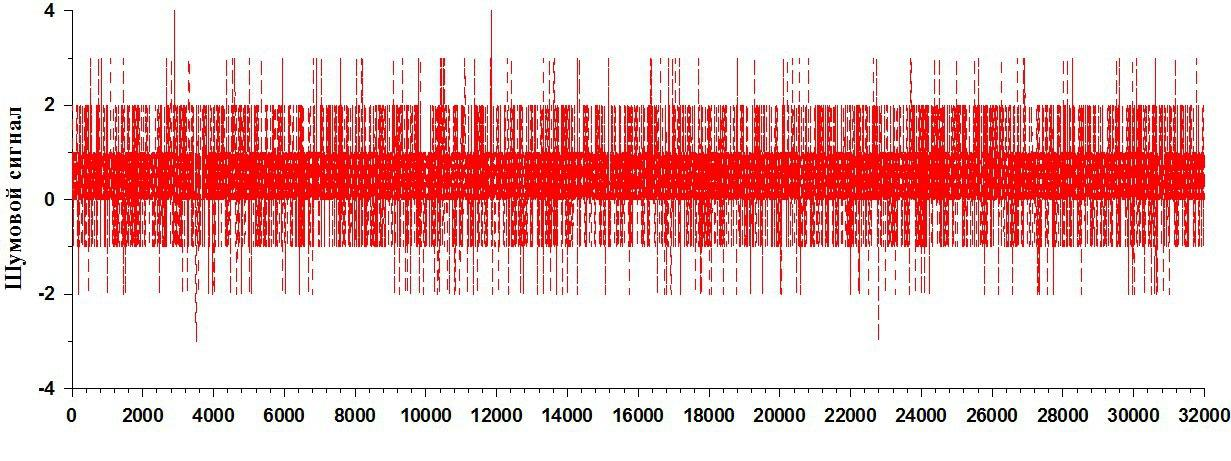
Теперь попробуем сделать тот же самый автокорреляционный анализ, что и с сигналами. Выполняем тоже самое: сдвигаем, все отчёты перемножаем, складываем и так далее до конца. Посмотрим как выглядит автокорреляционная функция шума. Обратите внимание, что у шума есть очень выраженный тонкий основной лепесток, а дальше нигде нет такого же четкого лепестка как в случае с сигналами.

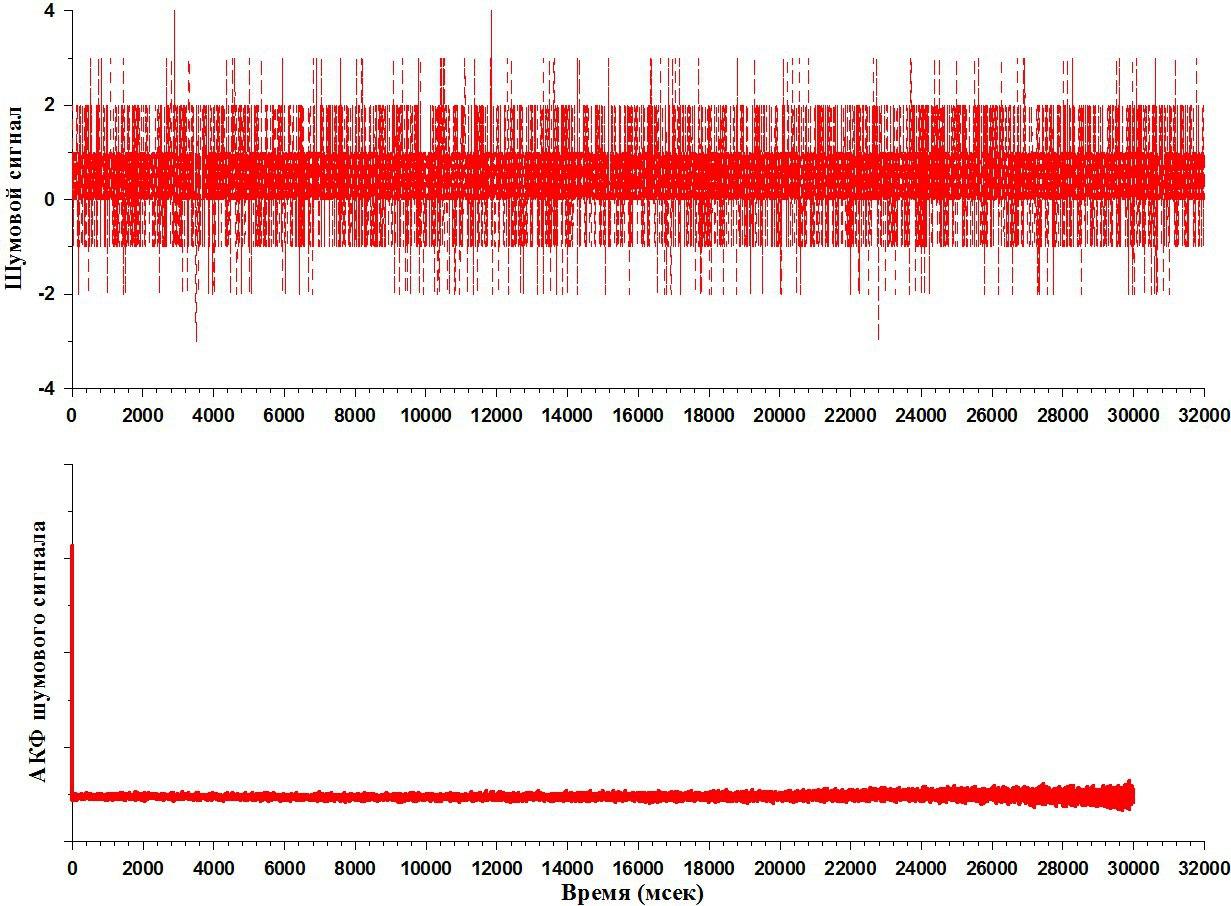
О чём это говорит? Это говорит о том, что шум не является периодическим, он каждый раз разный. Мы не можем найти период, на котором автокорреляционной функция опять выпрыгнет. Это очень интересное свойство шума. Надо сказать следующее: в зависимости от ширины автокорреляционной функции шума, как раз и классифицирует шумы, по-большому счёту.

Например, есть такой белый шум (левый рисунок ниже)- это шум, который не похож на себя никогда, то есть, если вы сдвигаетесь на один отчет, получаете вообще чистый 0. И дальше, сколько бы вы не сдвигали эту бесконечную шумовую дорожку относительно себя, вы получите опять 0. Поэтому можно зацепиться за тот момент, что белый шум имеет такие автокорреляционные свойства, и вы это четко видите.

Ещё есть окрашенные шумы, например, серый шум (правый рисунок ниже). Чем они фактически отличаются от белого? Приведем пример автокорреляционной функции серого шума.

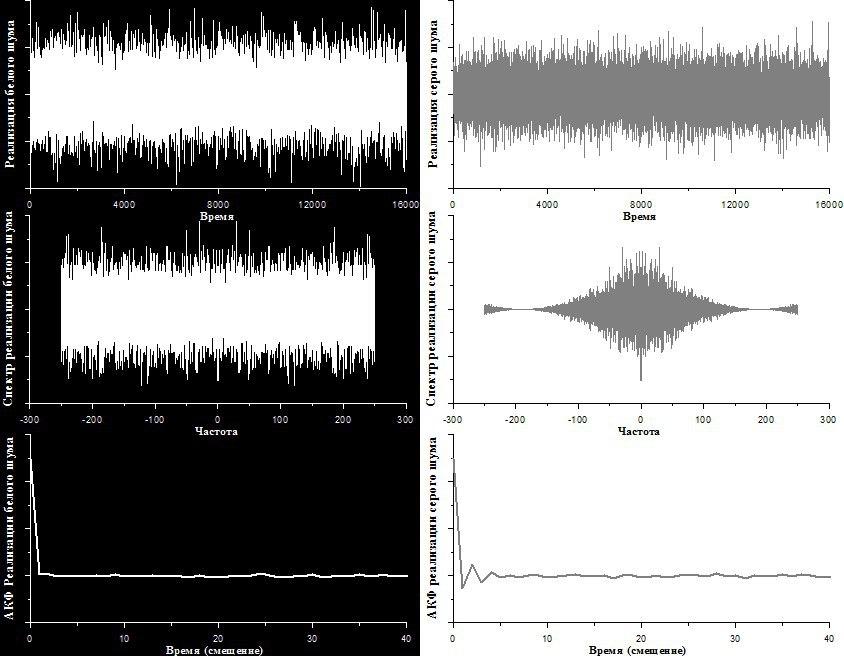
У серого шума автокорреляционная функция чуть шире, уже не 0. Фактически это белый шум, прошедшей через какой-то фильтр. Про теорию фильтров и элементы спектрального анализа поговорим немного позднее и посмотрим как эти две темы между собой дружат.

Итак, у нас в руках есть достаточно мощный инструмент анализа сигналов- автокорреляционная функция (АКФ). С точки зрения, программы-реализации вы видите, допустим на языке С, всего “10 строк кода”.

Программы, которые реализуют данную функцию, данный автокорреляционный анализ, можно сделать и компактнее. Способ достаточно простой, но достаточно эффективный.

Таким образом, если мы знаем модель сигнала, значит мы знаем его автокорреляционную функцию. С другой стороны, мы можем рассмотреть автокорреляционную функцию (АКФ) шума, и соотнести с автокорреляционной функцией принятого сигнала в эксперименте и в зависимости от того, как они соотносятся, например, по амплитуде и/или по ширине основного лепестка можем сделать вывод о наличии/отсутствии полезного сигнала, т.к. полезные сигналы в отличие от шумов, как правило, обладают какой-то конечной шириной основного лепестка АКФ.

Но когда мы работаем с сигналами, мы же сами хотим подобрать такую реализацию, которая бы была, что называется уникальной. То есть мы хотим подобрать такой сигнал, который сложно было бы сымитировать другим сигналом или помехой.

На этом можно играть, то есть можно придумывать такие сигналы, которые обладают какой-то уникальной автокорреляционной функцией. Дальше мы можем за это зацепляться и анализировать.

Например, вот наш какой-то сигнал, модель сигнала и её автокорреляционная функция.

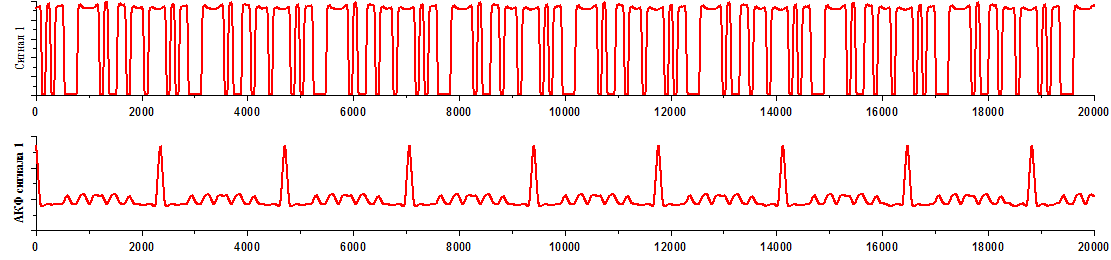
Вот другой сигнал, модель сигнала и её автокорреляционная функция.

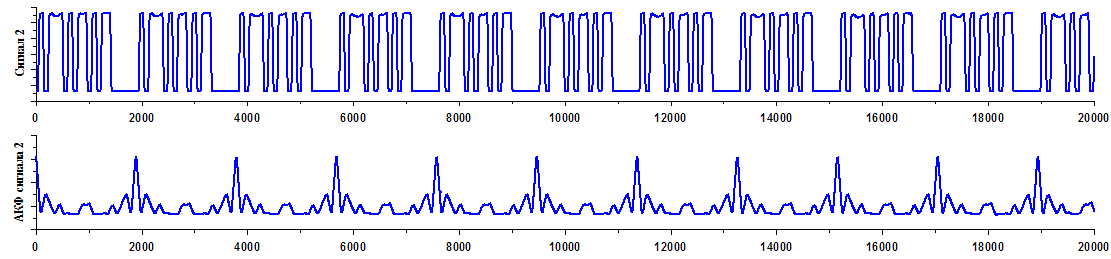
Обратите внимание, что несмотря на то, что сигналы отличаются, их автокорреляционные функции бывают и похожими. Но, мы то знаем, то что мы ждём на входе, поэтому мы можем пойти немножко дальше и “сворачивать сигнал”, не сам с собой, а с тем, что мы ожидаем. Привыкайте говорить “сворачивать”, далее я буду пользоваться этим выражением.

И вот теперь мы берем и сворачиваем сигнал друг с другом, взяли два сигнала и свернули их. По сути дела мы один сигнал сдвигаем относительно другого, опять перемножаем, суммируем и так далее. То есть строим эту корреляционную функцию. Теперь посмотрите насколько изменилась автокорреляционная функция.

Достаточно сильно амплитуда упала, и вы видите явные отличия. Таким образом, зная то, что мы ожидаем, тот сигнал, который мы ожидаем, мы можем существенно уменьшить влияние не только шумов, у которых автокорреляционная функция как вы видели, достаточно простая, но и влияние других сигналов. Другие сигналы будем называть помехами, будем существенно снижает влияние помех.

Такой интересный анализ можно выполнить с помощью автокорреляционной функции сигналов. Напомню еще раз, что именно биты является теми реальными импульсами, которые мы передаем и принимаем.

Рекомендую ознакомиться с методическими материалами к данной теме.

Для размышления

Попробуйте создать периодические и непериодические сигналы (например, u = sin (k*х) | u = c + k*х) и посмотреть, что получится, если пропустить такие сигналы, через автокорреляционную функцию, показанную на рисунке с кодом выше. Также ниже приведён пример автокорреляционной функции на Python.

Материалы

Методические материалы, где вы можете более подробно ознакомиться с автокорреляционной функцией, с корреляционным анализом.

• О сером шуме
• О белом шуме
• Сагалович Ю.Л. Введение в алгебраические коды. Глава 0.1 (немного о помехах в целом)