Возможности моделирования различных траекторий спутника на стенде «УНКС»

Продолжим знакомство с возможностями стенда «УНКС» и рассмотрим различные варианты движения «спутника».

Начнём с простого характера движения, когда «спутник» движется равномерно с одной и той же скоростью — равномерно-поступательно. Причём, для того чтобы показать насколько важно сопровождение «радаром» «спутника», мы повернём его в правую крайнюю позицию.

Мы сейчас задали расписание движения «спутника» по прямой с равномерной скоростью. Сначала «спутник» откалибровался и выставил себя на центр, а потом начал движение примерно со скоростью 5 см/с.

На рисунке 2 вы видите два графика. Сначала рассмотрим верхний: чёрная линия соответствует движению, заложенному в «спутник», то есть это программа его движения, по оси Х — время, по оси Y — координата x перемещения «спутника».

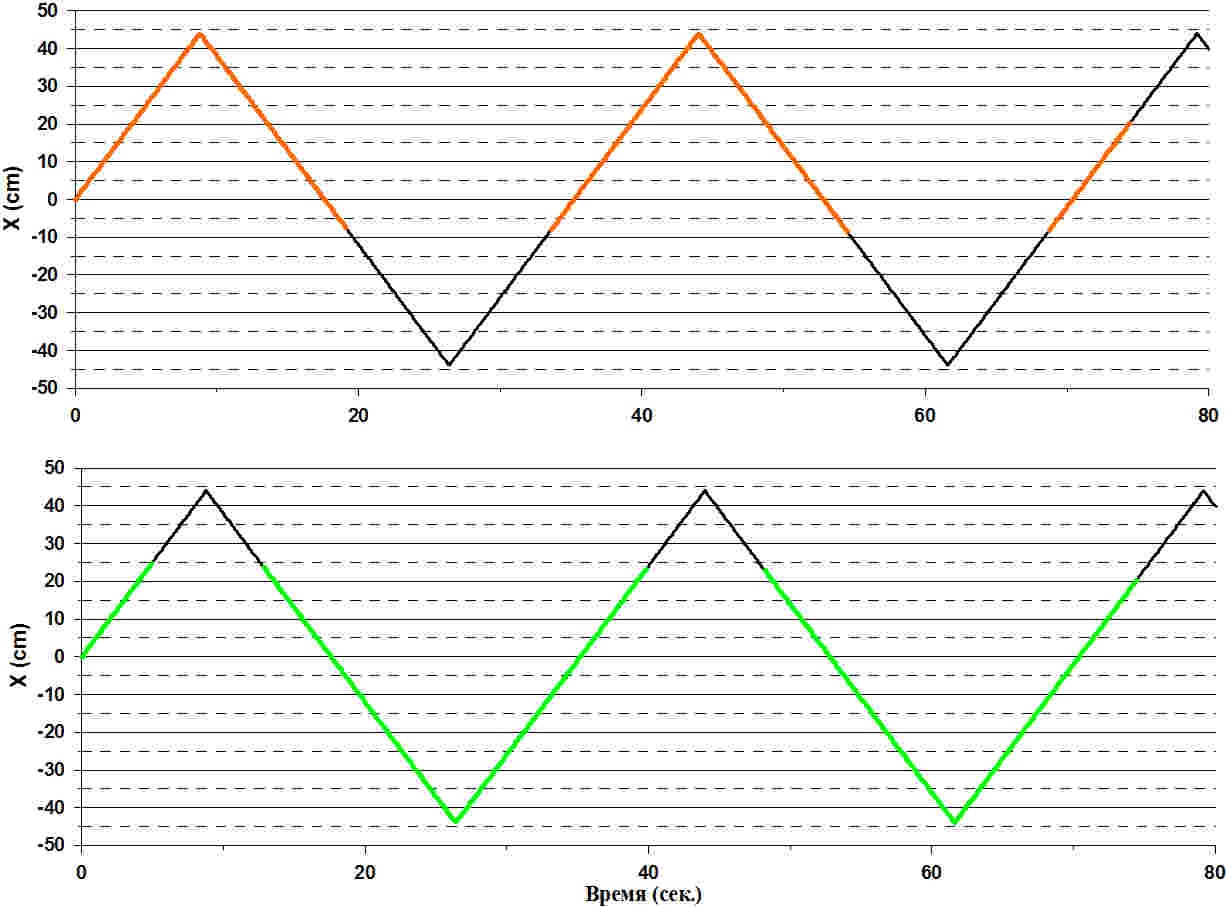
Давайте разберёмся, как ориентирована система координат, в которой движется «спутник». Фактически он движется вдоль x координаты, причём, начало системы координат установлено в центре направляющей. Когда «спутник» передал все данные, он возвращается в исходную центральную позицию, которая соответствует точке 0. Вот как раз на рисунке вы видите по оси Y, что график «спутника» пошёл от центра вверх до крайней точки своего маршрута, развернулся и с той же самой постоянной скоростью пошёл вниз. Обратите внимание, что оранжевым цветом показаны те моменты времени, когда «радар» принимал сигнал от «спутника». Фактически «спутник» при движении влево и вправо передавал свою позицию, и если на графике оранжевая линия заканчивается примерно на -10 см/с, то после этого момента «радар» перестаёт видеть сигнал «спутника». Таким образом, когда «радар» находится в правой крайней позиции, а «спутник» находится в левой части своего маршрута относительно «радара», то сигнал «радар» не видит, а когда «спутник» возвращается к позиции -10 см/с, то «радар» вновь начинает видеть сигнал.

Если развернуть «радар» в крайнюю левую позицию, то вы видите, что тоже есть слепые зоны. Мы запустили «спутник» по той же самой траектории: чёрная расчётная линия, но также возникает момент, начиная с которого, «радар» опять перестаёт видеть «спутник», но уже в правой части стенда.

Таким образом, мы с вами убедились, что «спутник» достаточно хорошо перемещается по расчётной траектории (чёрная линия на графике), а зелёная и оранжевая линии — это реальное положение объекта, которое измеряется при его движении по направляющей. И также вы видите, что есть слепые зоны, когда «радар» не видит сигнал от «спутника» совсем. То есть, если вы передаёте сигнал или данные в конфигурации, когда «спутник» находится в слепой зоне «радара», то «радар» эти данные не примет. Поэтому очень важно осуществлять точное сопровождение «радаром» «спутника».

Теперь посмотрим более сложный вариант движения. На рисунке слева приведён график движения спутника вокруг Луны, которая в свою очередь вращается вокруг Земли.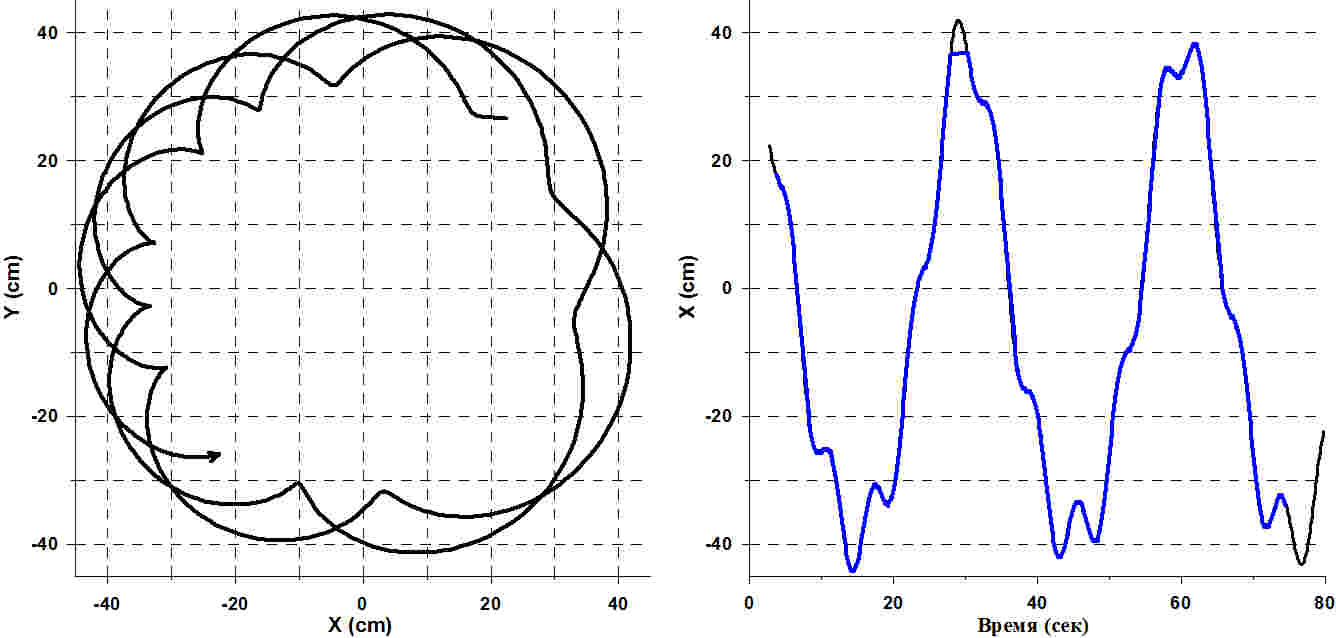 

Например, была такая интересная пара спутников GRAIL, которая изучала гравитационное поле Луны. И допустим, что этот искусственный спутник мы наблюдаем с Земли. Обратите внимание, что движение спутника относительно наблюдателя на Земле будет представлять достаточно сложную траекторию. Но наш «радар» находится в плоскости орбиты «спутника» и смотрит на траекторию только с позиции вдоль оси Х, то есть он видит только одну проекцию движения спутника. И если нарисовать эту самую проекцию, то она будет представлять чёрную линию на правом графике рисунка 3.

На нём возникает интересный характер движения, когда мы видим два периодических процесса: главный (с большой периодикой) и также периодику с меньшей амплитудой, но более высокочастотной, у которой небольшие пики связаны с движением спутника вокруг Луны, а большая общая динамика связана с движением Луны вокруг Земли.

Обратите внимание, что во время движения, «радар» смотрел в центр направляющей, вдоль которой движется наш «спутник», который отыгрывал динамику движения графика проекции на ось X. Несмотря на то, что «радар» смотрит в центр образующей, вдоль которой движется «спутник», всё равно на краях траектории есть положения, когда сигнал не регистрируется.

На графике синяя линия — это зарегистрированный сигнал, а чёрная — расчётное значение. И мы видим, что соответствие очень хорошее, то есть «спутник» движется чётко по расписанию, но в одном из мест пик как бы срезан, это означает, что «спутник» на краю правой части образующей попал в слепую зону, и сигнал мы не приняли на «радаре».

Вы видите, что характер движения может быть задан достаточно сложным, достаточно разнообразные варианты движения можно программировать. И, конечно, для успешного решения задачи трекинга, то есть сопровождения «радаром» «спутника» важно учитывать как раз характер движения. То есть если вы знаете, что объект движется по прямой, как в первом примере, и вы знаете, с какой скоростью он движется, то вы можете данный характер движения заложить в программу управления «радаром». Если вы знаете, как выглядит траектория движения и чему равны параметры движения аппарата вокруг Луны, то это тоже можно заложить в программу, которая управляет радаром. И это позволяет сильно повысить точность сопровождения, и как следствие качество принимаемого сигнала и полноту тех данных, с которыми вы работаете.

А как же быть со слепыми зонами, как с ними бороться, как там передавать данные и нужно ли их передавать, мы рассмотрим в следующий раз.

Для размышления

Попробуйте сами нарисовать возможные траектории движения реальных спутников. Затем поищите какие траектории бывают, по каким траекториям запускают современные спутники.

Материалы

• В чём состояла миссия GRAIL