Определение углового ускорения вращения шестеренок стенда «ОВКС»

Лебедев Валентин Павлович
кандидат физико-математических наук, старший научный сотрудник Института солнечно-земной физики СО РАН
Характер движения шестерёнок можно задавать достаточно свободно, и запустить их с равноускоренным или равнозамедленным ускорением не составляет труда. Но решить обратную задачу: по измеренному сигналу определить угловое ускорение — уже гораздо сложнее.
#ТБС #ОВКС
Продолжим разбирать задачи, которые были предложены на Олимпиаде НТИ на треке “Технологии беспроводной связи”. В прошлых темах мы сосредоточились на задачах - определить код Хэмминга, который зашифрован на каждой шестерне, а также определить период вращения шестеренок.
А
сейчас мы разберем следующую задачу -
определить
угловое ускорение вращения каждой
шестерни. Дело
в том, что характер движения шестерёнок
можно задавать достаточно свободно, и
запустить их с равноускоренным или
равнозамедленным ускорением не составляет
труда. Но решить обратную задачу: по
измеренному сигналу определить угловое
ускорение уже гораздо сложнее. Для того,
чтобы задача решалась методами школьной
математики, давался файл данных, который
соответствовал равномерному вращению,
то есть вращению с одной и той же угловой
скоростью.
Итак, какие данные были предложены для решения этой задачи.
На
видео можно видеть, что шестерёнки
вращаются равномерно. Фотодиод
регистрирует сигнал в этом режиме,
данные записываются в файл (который
выдавался участникам трека). Шестеренки
вращаются довольно долго: около тридцати
двух секунд, это необходимо, чтобы был
достаточно представительный набор
данных.
Далее шестерёнки запускаются с постоянным угловым ускорением, которое не известно нам заранее, и которое необходимо определить по тем данным, которые будут получены в результате работы стенда. Обратите внимание, что вращение равноускоренное. Вращение начинается с малой угловой скорости, и постепенно она увеличивается. Также по характеру вращения, можно заметить, что малая шестерня совершает намного большее, чем количество оборотов в единицу времени, чем количество оборотов, которое совершает большая шестерёнка. Соответственно ускорение у малой шестерёнки должно быть больше, чем у остальных, а у большой — самое малое. Когда вы делаете какие-то свои выводы, вы должны учитывать все условия задачи, даже те, которые сформулированы неявно.
Сначала рассмотрим сигнал, полученный при равномерном вращении.
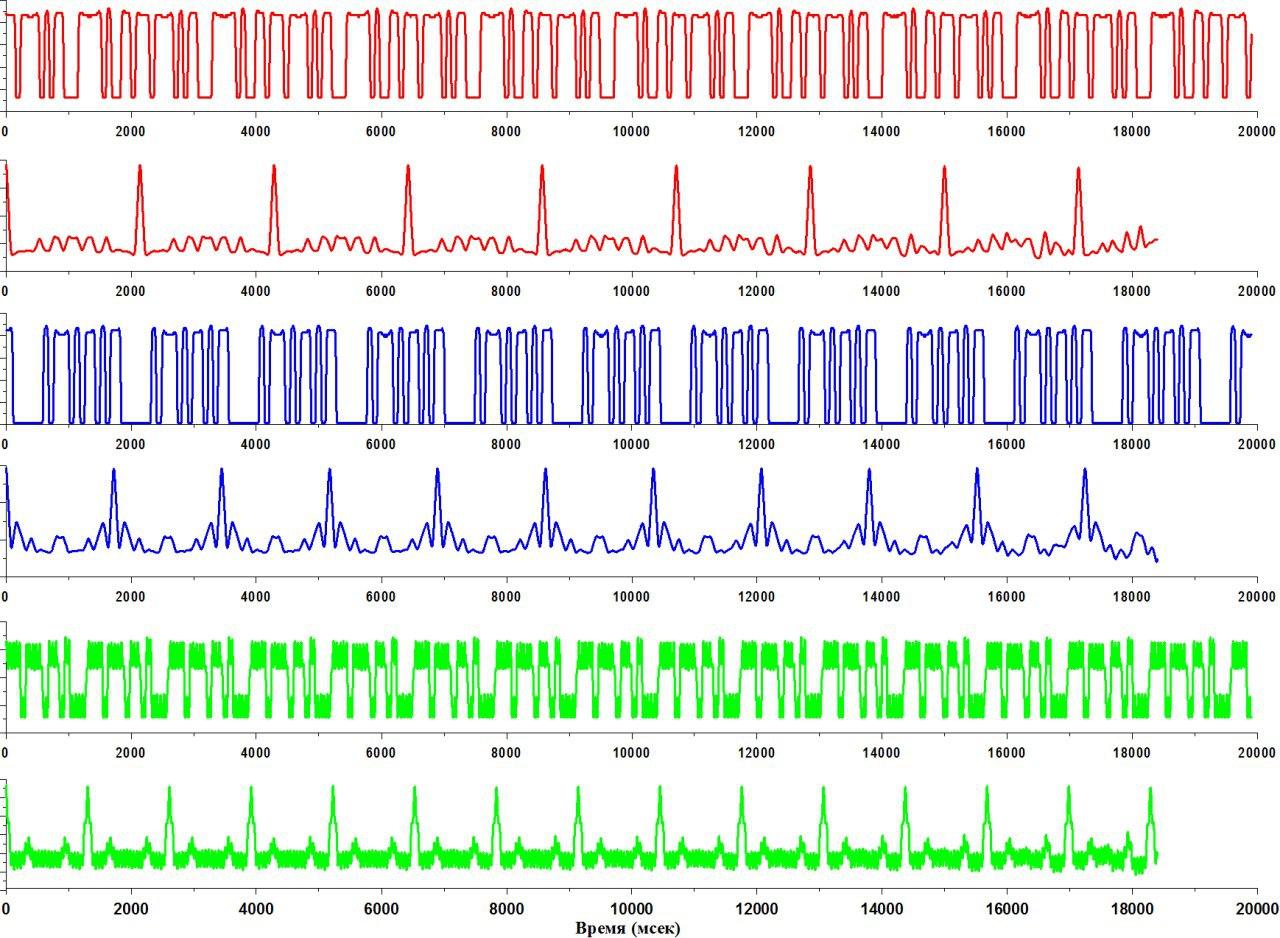
Красный
график соответствует большой шестерне,
синий — средней, зелёный — малой. Перед
вами также приведены графики
автокорреляционной функции, и по пикам
этой функции можно уже определить период
вращения каждой шестерни, а также мы увидели
до этого, что период вращения находится
в том же самом отношении, что и радиусы
шестерёнок, поскольку они в жесткой
сцепке.
Теперь посмотрим, как выглядит сигнал, когда шестерни вращаются равноускоренно.
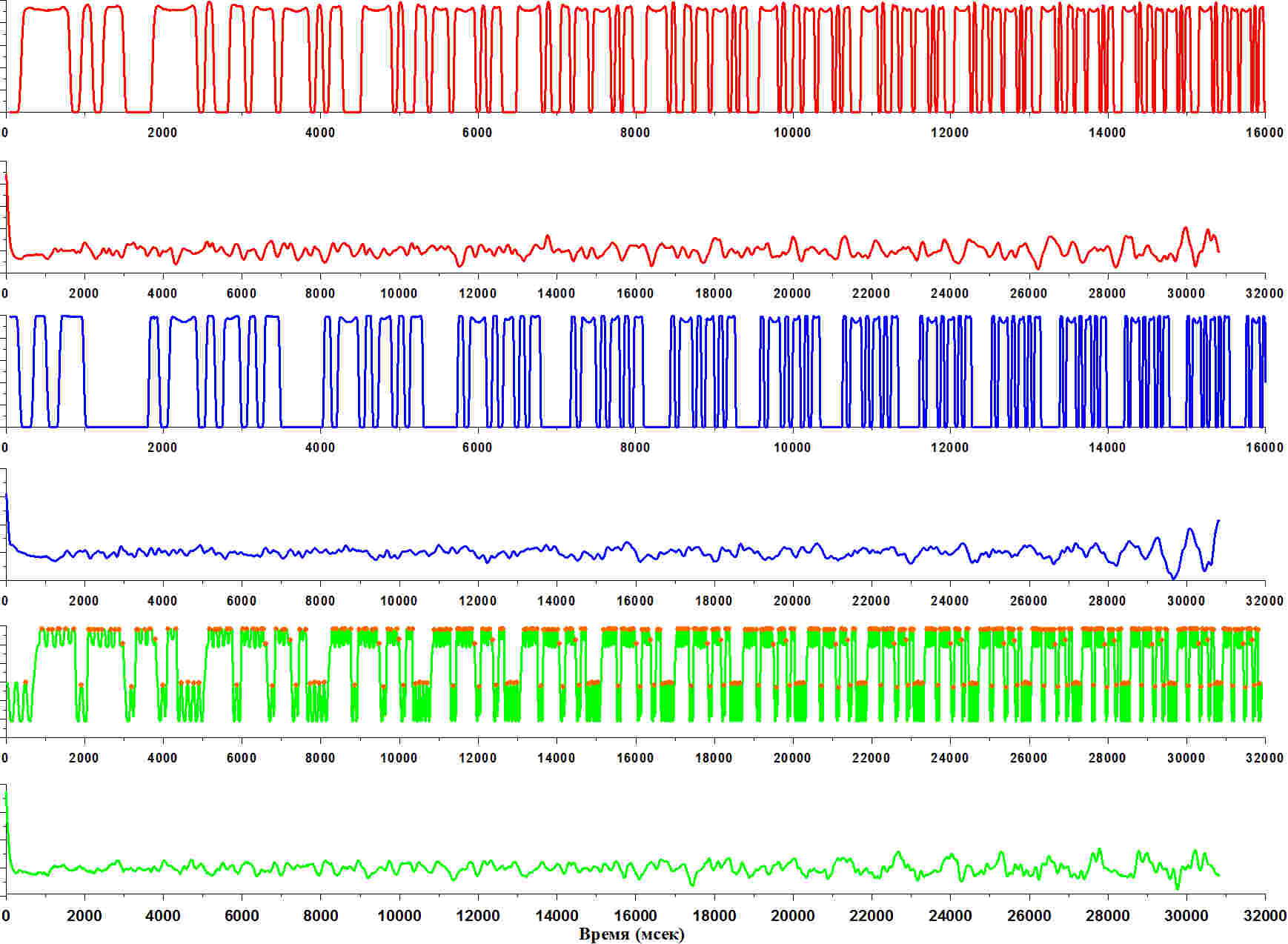
На
этом рисунке видно, что сначала один
оборот занимал много времени, но с
ускорением этот интервал обращения
вокруг своей оси становится всё короче.
И в самом конце, когда шестеренка
останавливается - этот интервал времени
обращения шестеренки вокруг своей оси
уже самый короткий.
Чтобы решить задачу строго и в общем случае, нам нужно было выделить интервал, на котором шестерня совершает один полный оборот. При этом нужно было каким-то образом считать импульсы и в дальнейшем пытаться через время изменения одного периода определять ускорение вращения каждой шестерёнки. В таком случае задача очень сложная. И как-то проще её решить, как, например, при решении задачи определения периода вращения с помощью автокорреляционной функции по её пикам, тоже не просто. Потому что, если построить график автокорреляционной функции в этот раз (нижние графики соответствующих цветов), то никаких пиков здесь не наблюдается, то есть сигнал не похож на себя ни в какой части: как бы мы не сдвигали исходный сигнал относительно себя, он не найдёт никакого подобия.
Это и понятно, потому что период всё время уменьшается. И вы видите, что автокорреляционная функция для каждого из сигналов имеет четко выраженный пик вначале, когда сдвижка равна нулю, а далее за несколько миллисекунд падает практически до нуля, и далее идут шумовые флуктуации, по которым ничего определить нельзя.
Что же делать в этом случае? Можно попытаться решить задачу глобальным фитированием, то есть перебором всех параметров, но давайте посчитаем сколько параметров нам придётся учесть: угловое ускорение, начальная угловая скорость для каждой шестерни, ещё и фаза, а нам не дано в задаче, в каком фазовом соотношении находятся коды на каждой из шестерёнок, то есть они могут начинаться с любой фазы. Итого получается три неизвестных параметра для каждой шестерни, а для трёх шестерней получается девять.
И такой глобальный перебор займёт много времени и не является достаточно точным. То есть задача получается достаточно сложная. А на олимпиаде задачи должны решаться достаточно быстро, и для задачи подобного рода среднее время решения составляет порядка десяти минут.
Таким образом, нужно искать какой-то путь, который позволил бы уменьшить как количество неизвестных, так и упростить способ решения.
Мы можем вспомнить, что шестерёнки находятся между собой в определенном соотношении, которое определяется радиусами данных шестерёнок. А это соотношение можно определить как раз по файлу, в котором содержаться данные, соответствующие равномерному вращению.
Итак, допустим, теперь это соотношение у нас есть. Осталось определить какое-то стартовое ускорение, то есть если мы определим угловое ускорение вращения одной из шестерёнок, то и вычислим угловые ускорения вращения у каждой из двух оставшихся.
За что можно зацепиться при решении этой задачи?
Ранее в видео об устройстве стенда ОВКС уже говорилось, что светодиод и фотодиод не точечные, а занимают некоторое место, а также мы видели, что сигнал, который модулируется малой шестерёнкой и потом снимается её фотодиодом, определяется не только характером узора на ней, но и зубчиками шестерёнки, которые периодически открывают и закрывают фотодиод. Не составляет труда подсчитать сколько зубчиков у малой шестерёнки — их 25 штук. Узор внутри малой шестерни имеет всего 15 элементов (как было определено в предыдущей теме). Таким образом, самые быстрые изменения связаны с этими зубчиками. А ещё они дают на графике чёткие пики. И если “зацепиться” за эти пики (они обозначены оранжевыми точками) и определить их положение (это довольно просто решается на уроках по информатике), то можно проанализировать временной интервал между пиками, то это даст достаточно информации для того, чтобы можно было определить угловое ускорение вращения. Ещё стоит обратить внимание, что зубчики образуют периодический узор, то есть повторяются, а узор внутри шестерёнки имеет достаточно апериодичный характер, и поэтому с зубчиками иметь дело проще.
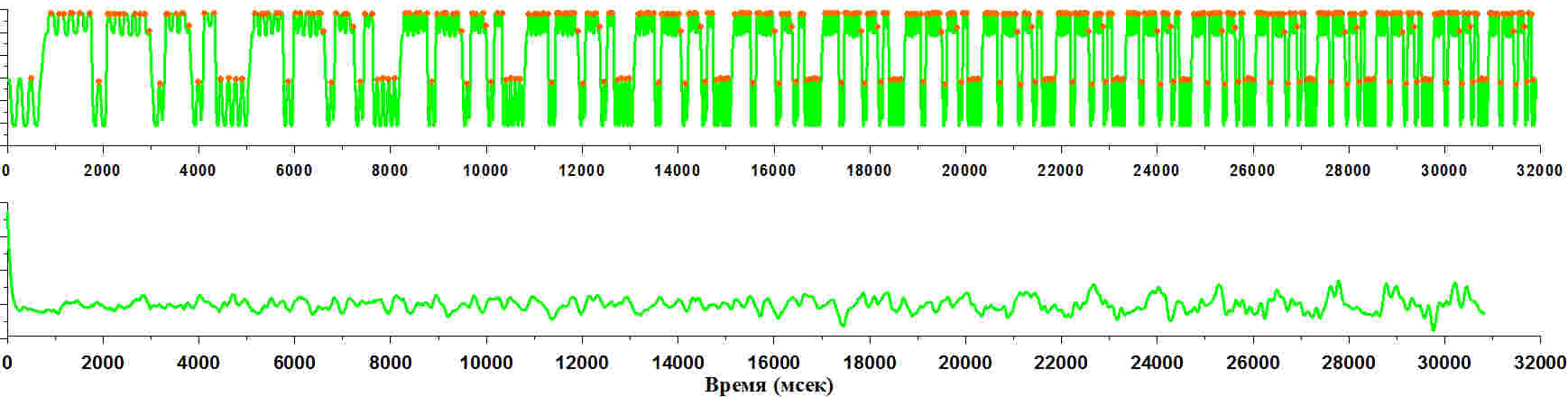
Итак,
если известно количество зубчиков,
можно определить их положение в сигнале,
таким образом мы узнаём, что расстояние
между зубчиками равно одной двадцать
пятой периода. Тогда дальше можно
предположить, что на интервале времени
между двумя пиками, даже если шестерёнка
вращается медленно, то скорость вращения
это примерно 1/25 секунды, что примерно
равно 40 миллисекундам, и на этом интервале
скорость вращения можно считать близкой
к постоянной. Таким образом, мы с вами
можем построить следующий график.
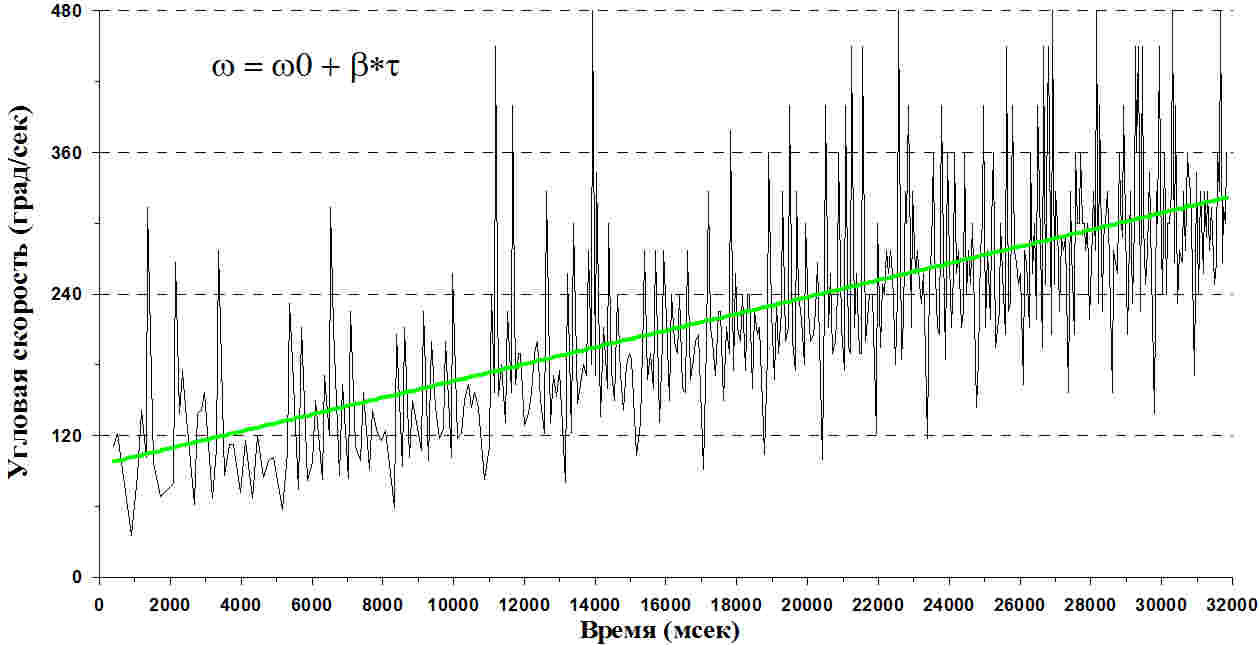
Обратите
внимание, что здесь много точек, который
расположены на плоскости, где по оси
икс отложено время, по оси игрек —
угловая скорость вращения, вычисленная
по временному интервалу между двумя
пиками, которые соответствуют времени
прохождения между двумя зубцами
шестерёнки. А мы знаем что равноускоренное
движение — это равномерное увеличение
угловой скорости вращения, которая
определяется формулой ω = ω0 + β⋅τ, фактически
это линейная зависимость от времени, а
наклон этой кривой это и есть угловое
ускорение.
Но обратите внимание на следующий интересный момент, что динамика, которая обозначена чёрной линией, содержит достаточно много шумов (всплесков/пиков), это связано с тем, что зубчики не идеальные, разные, но тем не менее общий характер этой функции виден — прямая линия в среднем. Фактически нужно как-то вписать наилучшим образом в эти данные прямую линию. А данную задачу можно решить с помощью метода наименьших квадратов, который очень широко используется при анализе тех данных, с которыми вы работаете. Этот метод будет рассмотрен в следующем занятии.
Сейчас построить линию нужно так, чтобы средний квадрат расстояния от этих точек до искомой линии был бы минимальный. То есть минимизировать такую среднеквадратичную ошибку при вписывании прямой линии.
Считаем, что мы это сделали и получили зелёную прямую, нужно определить её наклон, который соответствует бетта. И в результате, если выполнить все эти действия, то окажется, что, действуя таким образом, можно определить угловое ускорение вращения с точностью лучше, чем один градус за секунду в квадрате (1°/с2). Такая точность являлась требованием при решении предложенной задачи.
Для размышления
Вычислить угловое равнозамедленное ускорение для предложенных данных.