Период вращения шестеренок стенда «ОВКС»

Продолжаем цикл занятий посвященных задачам предложенным на треке “Технологии беспроводной связи” в Олимпиадах предыдущих лет.  Первую задачу - определение кода на шестерни - рассмотрели в предыдущей теме. Следующая задача, которая очень близка к первой, это определение периода вращения шестеренок. 

Вообще говоря, когда работают с сигналами, как правило, работают с какими-то циклическими процессами. И на практике приходится часто сталкиваться с определением периодов каких-то характерных процессов. В данном случае в задаче нужно было определить период вращения каждой из представленных шестеренок.

Давайте запустим стенд на стандартных настройках. За движением шестеренок можно наблюдать в видео. Пока шестеренки вращаются, можно следить за белой точкой, это своеобразный маячок. Даже просто смотря за этим белым маячком, можно прикинуть примерно каков же период вращения, допустим, большой шестеренки. Если следить внимательно то можно заметить, что период вращения у большой шестеренки самый большой, у средней поменьше и у малой шестеренки самый маленький период обращения. Это  уже некая дополнительная информация. Дальше если примерно оценить радиус этих шестеренок, и помнить, что отношение радиусов есть отношение их периодов, то это тоже будет являться дополнительной проверкой, того насколько точно будет определен ответ в дальнейшем. Эту задачу можно решать с двух сторон: определив отношение радиусов и непосредственно анализируя сигнал можно понять, как же медленно или быстро они вращаются. Для того, чтобы определить период вращения каждой шестеренки, даже если померены их радиусы, нужно определить период вращения хотя бы одной. Давайте попробуем это сделать. 

Что такое корреляционный анализ и  автокорреляционная функция? Посмотрим на графики - красную, синюю и зеленую последовательность импульсов, которые соответствуют динамике сигнала, который принимает фотодиод (верхние графики соответствующих цветов). 

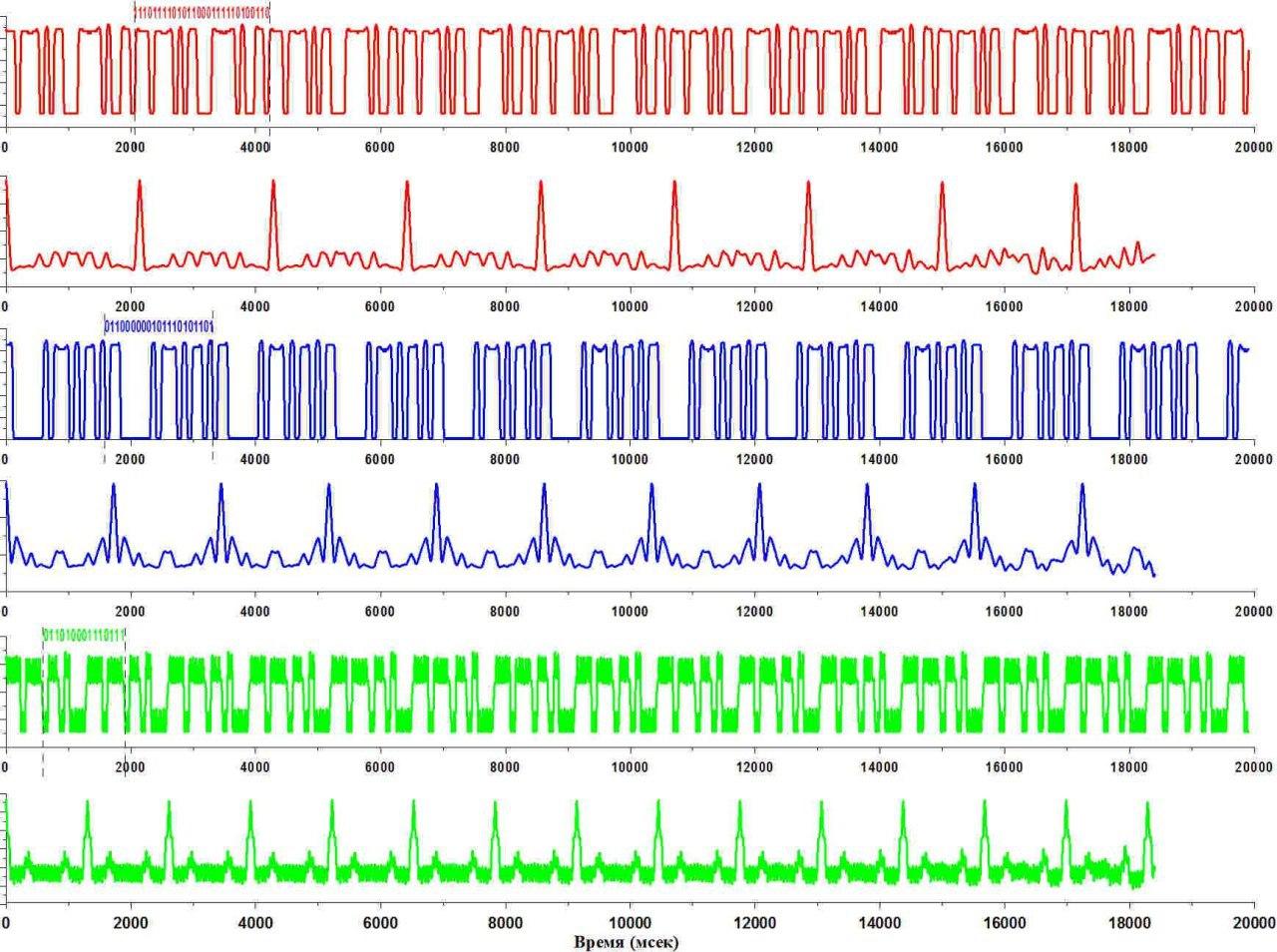
Из графиков четко видно периодичность. Например, можно следить за каждой крупной частью импульсов, это очень наглядный маркер. Определить период вращения задача интересная. Можно использовать много различных подходов , можно искать какое-то подобие, находить какой-то паттерн в данных, а можно воспользоваться автокорреляционным анализом. Что такое автокорреляционная функция? 

Возьмем, например, красный сигнал сдвинем на один отсчет относительно себя, допустим вправо на один отсчетчик сдвинулись, перемножили свдвинутый и не сдвинутый сигнал, просуммировали и поставили точку. И если действовать так далее - то есть сдвигать, перемножать и суммировать, сдвигать, перемножать и суммировать,  …., то получим функцию представленную на нижнем красном графике. 

Обратите внимание, что у этой функции есть четко выраженные пики. Их видно невооруженным взглядом. А что происходит со сдвинутым сигналом, когда в автокорреляционной функции мы видим четкий пик? Это означает, что сдвинутый и не сдвинутый сигнал с точностью до периода совпали, то есть они подобны и дальше идут одинаково. Это означает, что найдена сдвижка на один период. Сдвинем еще, то есть сдвинутый уже на два периода отличается от исходного и тд. Определить максимум этой автокорреляционной функции задача уже достаточно простая. Определяем время каждого пика, находим между ними разницу и, по сути дела,  период определен. Дальше можно поступать следующим образом: можно считать эти пики и делить на общее время или же можно посмотреть разницу этих самых времен, все их опять сложить и поделить на их количество, то есть найти средний период обращения. 

Продолжение задачи по определению периода заключается в том, чтобы найти насколько нестабильно вращение. Реальная система никогда не бывает с идеальным бесконечным близким вращением. Бывают небольшие люфты, которые приводят к тому, что период обращения может немного меняться. Анализируя расстояния между пиками автокорреляционной функции, можно определить как раз эту неточность обращения. В данном примере установка собрана очень хорошо - неточность обращения соответствует порядка 2 миллисекундам. По графикам можно понять, что значит 1 миллисекунда относительно периода. Видно, что на красной автокорреляционной функции первый пик соответствует 2100 миллисекунд или 2,1 секунды и тд. Неточность положения периодов примерно 2 миллисекунды, а сам период 2000 миллисекунды, то есть неточность соответствует 0,1 процента. Таким образом, период вращения достаточно стабилен. 

Такой же анализ можно выполнить и для средней шестеренки. На нижнем синем графике представлена автокорреляционная функция соответствующая сигналу от средней шестеренки, который представлен на верхнем синем графике. На автокорреляционной функции можно четко увидеть пики. Вспоминаем, что пик соответствует сдвижке на один период, значит сигналы совпадают.  Даже на глаз видно, что количество синих пиков больше, чем количества красных, т.е. период обращения меньше. Если посмотреть внимательно, то период обращения средней шестеренки (которой соответствует синий сигнал) составляет примерно 1,7 секунды. 

Дальше смотрим на зеленый сигнал (верхний зеленый график), который соответствует малой шестерне.  Видно, что несмотря на то, что есть характерная изрезанность (характерная “борода”) поверху и понизу сигнала, она нисколько не помешала автокорреляционной функции (нижний зеленый график) иметь четкие пики. Их количество больше, чем синих и красивых пиков, то есть период обращения малой шестерни самый маленький и соответствует примерно 1,3 секунды. 

Далее если найти отношение между диаметрами или радиусами данных шестерней, то будет видно, что они находятся в том же самом отношении, что и найденные периоды. Это всегда очень полезная проверка. Если что-то можно проверить, то лучше проверить особенно в каких-то практических задачах. 

Материалы данного занятия будут использоваться при решение задачи, когда характер движения шестерни более сложный, более интересный, например, равноускоренное движение.

Для размышления

Вспомните максимально возможное число процессов в жизни и технике, в которых применимо понятие периода?

Материалы

• Немного о периодах вращения планет