Код на шестеренках стенда «ОВКС»

Разберем несколько задач, которые были предложены на треке Беспроводные технологии связи в 2017–2019 годах. Это были самые первые, самые простые задачи, они посвящены введению в тему «Помехоустойчивое кодирование» и «Знакомство с кодом Хэмминга».

Эти задачи решались на стенде с шестеренками. 

Задача состоит в следующем: если внимательно посмотреть на шестерёнку, то на ней можно увидеть узор из окошечек и стенок.  Этот узор представляет собой последовательность 0 и 1 (стенки — 0-ки, окошки — 1-ки). 

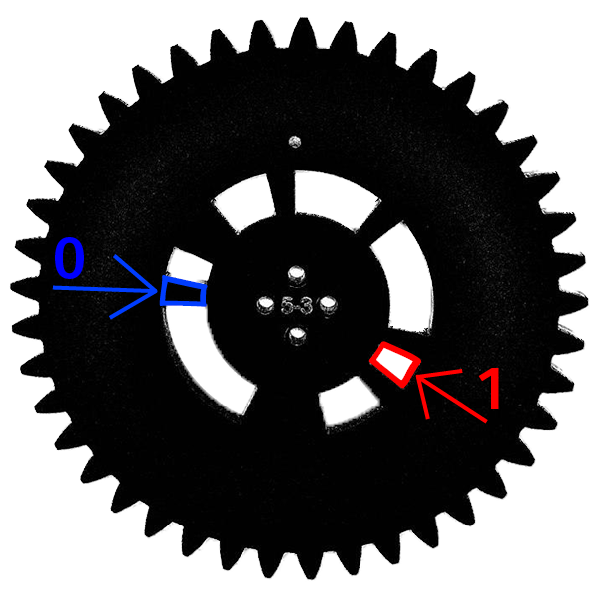
Нужно, внимательно проанализировав данный узор, понять какой код Хэмминга закодирован на каждой из шестерней.

Условие задачи было следующее: нужно было разгадать код при условии, что данный код на шестерёнке записан без ошибок, то есть все 0 и 1 находятся на своих местах, или синдром равен 0.

Для решения этой задачи необходимо внимательно изучить, где начинаются и заканчиваются стенки и окошки, исходя из этого, определить длину кода и потом определить, как же он устроен.

Для решения задачи можно внимательно проанализировать узор шестерёнок, но можно решить задачу и с помощью анализа сигнала, который получается в результате работы стенда.

Перед запуском стенда - выставляем параметры уже настроены: период вращения 2,1 с, время работы 20 с и уровень сигнала, который излучается светодиодом, на всех шестернях одинаков.

Записываем настройки в стенд и запускаем.

Шестерёнки вращаются, модулируется сигнал вращением этих шестерёнок, через 20 с они остановятся, и мы увидим как выглядит тот сигнал, который зарегистрировал фотодиод.

Вы видите на данном графике, что разный цвет соответствует сигналу с разной шестерни. Можно работать уже сразу с данным сигналом, а можно взять непосредственно файл с данными, с которым можно работать.

Вы можете видеть, что здесь есть четыре столбика. Первый называется тик. Тик — это один отчет по времени, который составляет 2 миллисекунды, то есть разница между двумя соседними строчками составляет 2 мс. Далее идут три столбика, которые озаглавлены ПД1, ПД2, ПД3 — это соответственно сигналы с каждой из наших шестерней, то есть это именна та числовая информация, которая до этого была представлена на графике.

Итак, давайте посмотрим как можно решить эту задачу и с какими сложностями можно столкнуться.

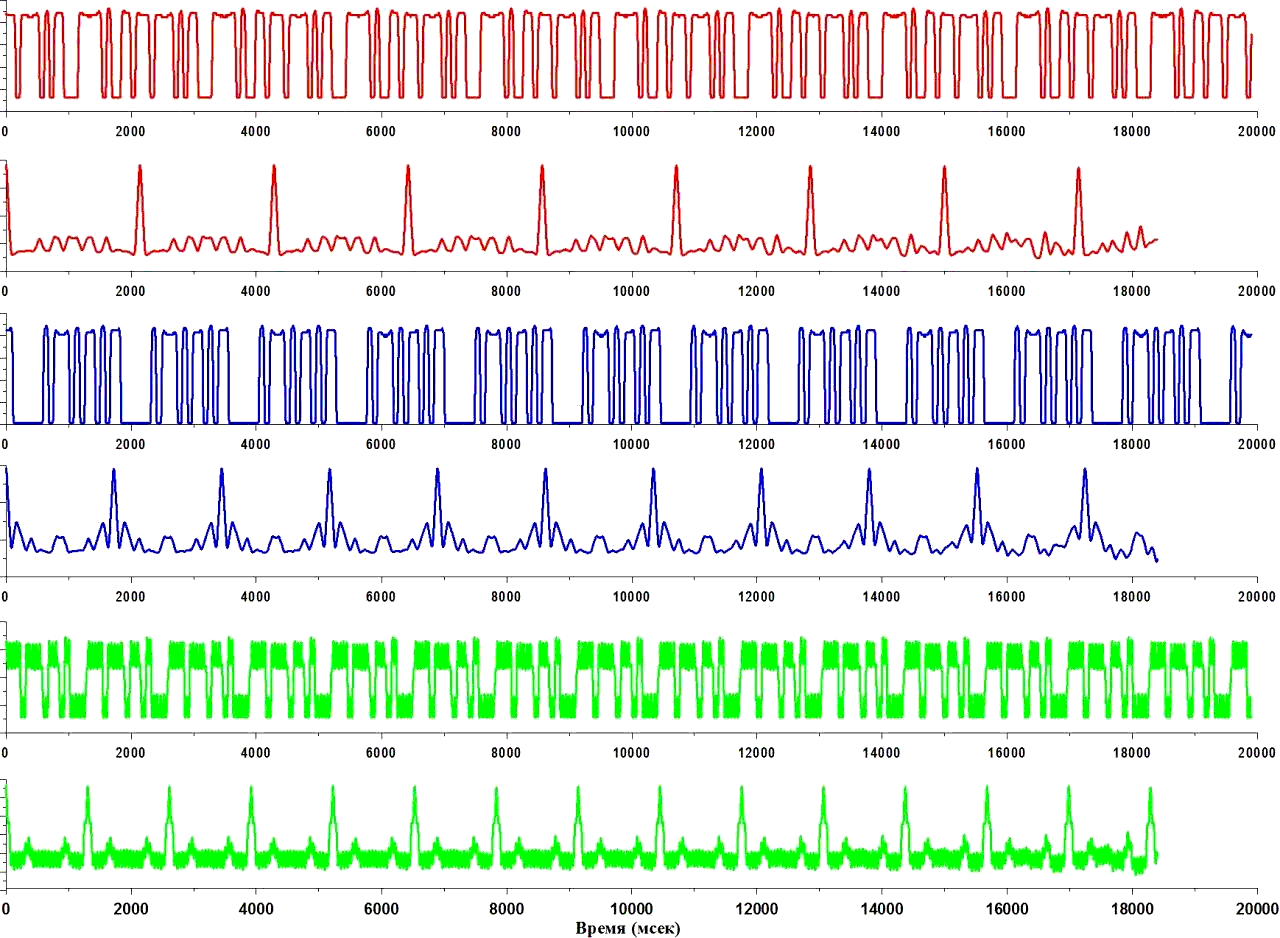
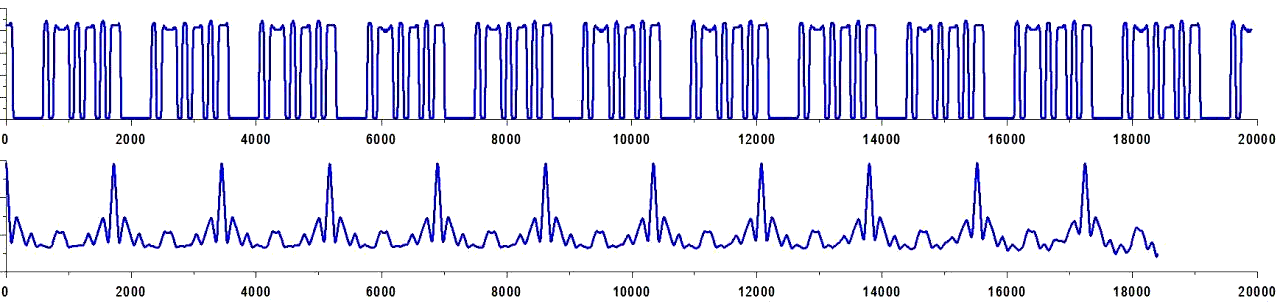
На данном графике представлен сигнал с каждой из шестерёнок, только разнесены они подальше друг от друга, чтобы было удобно работать с данными. Красный график — это сигнал с большой шестерёнки, синий — со средней шестерёнки, зелёный — с маленькой третьей шестерёнки, на котором видны характерные сигнальчики по верху и по низу, как будто это шум, на самом деле это модуляция, вызванная зубчиками шестерёнки.

Давайте разберёмся с тем, что получили, на примере большой шестеренки (красный сигнал на графике). На графике нижние значения (нулевой уровень) соответствуют 0-ям, верхние значения (максимальный уровень) — 1-ам. И на всём графике можно обнаружить код, который спрятан на большой шестерне. Начало кода отмечено белой точкой на самой шестерёнке.

 

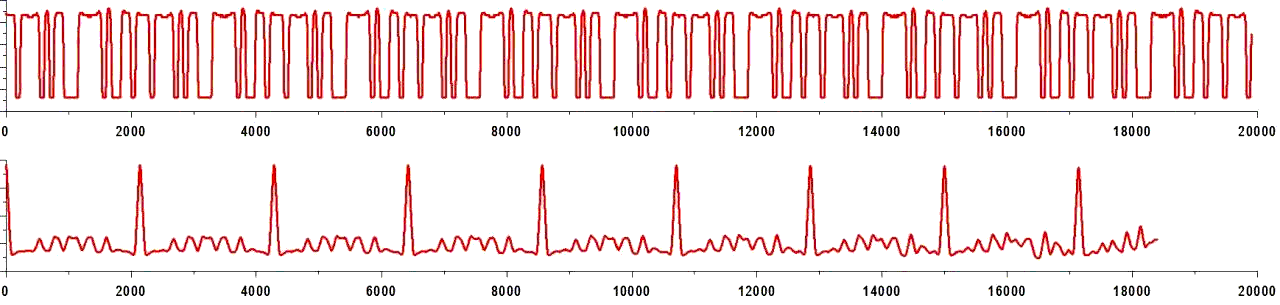
На шестерёнке видно, что белая точка стоит в начале большого окошка, а слева от неё маленькая стеночка. Примерно можно определить на глаз, что окошко шире в три раза чем стенка. Если сопоставить это с графиком, то есть найти короткий низ и примерно втрое больший верх, то это и будет начало.

А дальше остаётся тем же самым образом проанализировать весь оставшийся узор и график. Шестерёнка вращается против часовой стрелки, но узор относительно вас меняется последовательно слева направо, как бы по часовой стрелке. Соответственно мы видим сначала широкое окошко — это три 1, дальше короткую стенку — это один 0, далее ещё большее окошко — это четыре 1 и так далее. Если внимательно и аккуратно проинтерпретировать всю последовательность, то получим: 111011110101011000111110100110.

 

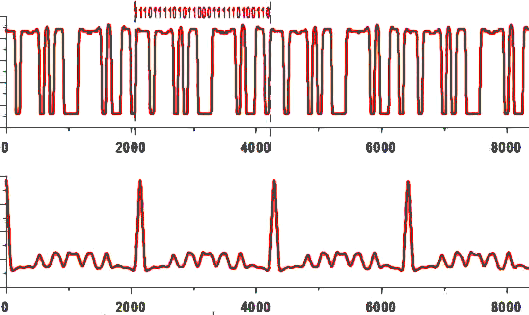
Причём, когда решается такая задача, то нужно проверять своё решение на как можно большем количестве примеров. В данном случае у нас имеется узор — это раз, и имеем полученный сигнал — это два. И при решении этой задачи её могут решать, например, одновременно два человека: первый анализирует узор на шестерёнке, а второй — график полученного сигнала. И если результаты у них совпадут, то решение скорее всего верное. То есть, таким образом, используется идеология помехоустойчивого кодирования: если есть возможность проверить, то проверяем.

Давайте разберёмся со второй шестерёнкой. Обратите внимание, что средняя (вторая) шестерёнка, в отличии от большой, будет вращаться по часовой стрелке. Таким образом, фотодиод будет считывать сигнал по направлению вращения — против часовой стрелки. То есть, если разработчик этих шестерней записал код на всех шестерёнках относительно начала (белой точки) по часовой стрелке, то при вращении со второй шестерёнки сигнал будет читаться в обратном направлении — справа налево. В данном примере так и сделано для наглядности: все коды на все шестерёнки записаны в одном направлении по часовой стрелке.

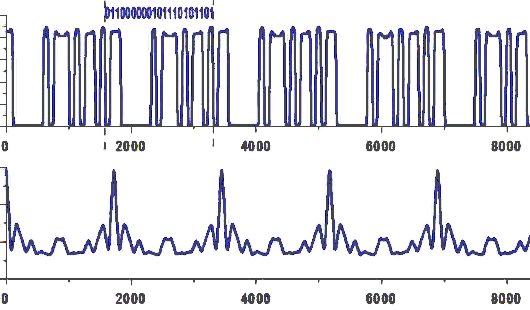
Посмотрите внимательно на синий график и на среднюю шестерёнку.

Можно найти характерное начало, где слева от точки лежит короткая стенка и справа — самое короткое окошко, справа от которого расположена ещё одна короткая стенка. На графике мы видим три таких элемента, но только один из них будет соответствовать коду (узору) на этой шестерне. И если проследить внимательно всю последовательность, то код Хэмминга читается наоборот — справа налево.

 

Осталось рассмотреть малую шестерёнку. 

 

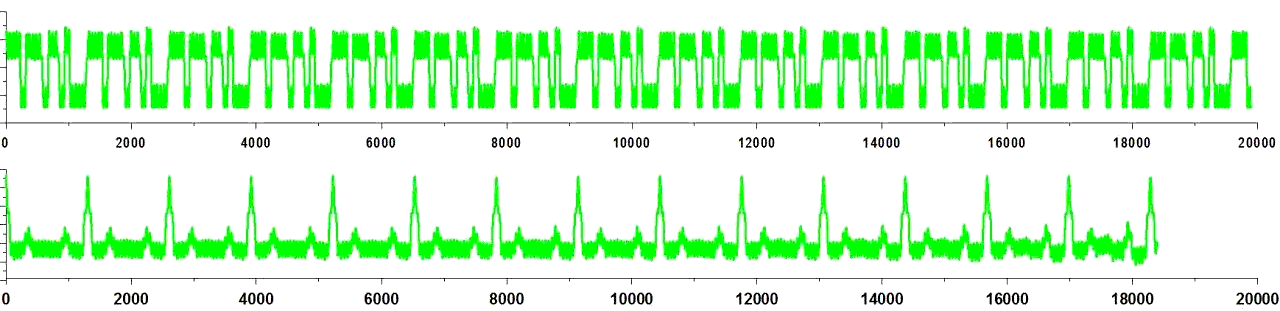
Обратите внимание, что она вращается в том же направлении, что и большая. Это означает, что код можно читать слева направо. Опять находим положение начала — белую точку, и видим с одной стороны от неё три 1, с другой — один 0. Попробуем прочитать теперь последовательность слева направо: 0, две 1, 0, 1, четыре 0 и так далее ( 011010000…). Восстанавливаем код Хэмминга на данной шестерёнке и получается, что его длина 15.

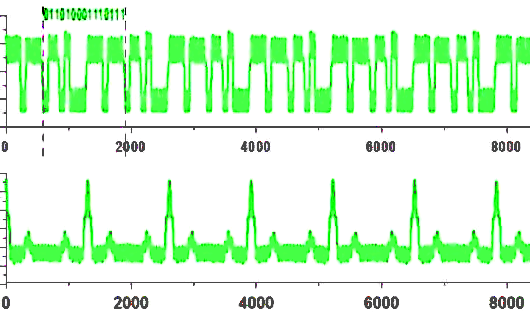
Конечно же могут быть какие-то неточности при восстановлении ноликов и единичек. Так как при работе с реальным сигналом может в действительности оказаться, что ширина окошек и стенок не везде одинаковая, то есть они могут немного отличаться между собой. И из-за этого могут возникнуть вопросы, например, посчитать какую-то стеночку за два нуля, хотя на самом деле там один ноль. И когда вы внимательно работаете с данными, принимаете решение с какой точностью эти окошки и стеночки сделаны, то вы итеративным образом определяете, что там закодировано на самом деле.

И подсказка о том, что вы делаете всё правильно, это когда вы определили код Хэмминга, который не содержит ошибок.

Для размышления

Напишите код зашифрованный на шестерёнке, представленной на рисунке:

Материалы

• Код Хэмминга. Пример работы алгоритма
• Коды Хэмминга — Григорий Кабатянский