Чистая дилемма (ОКД НТИ 20/21 :: ИЭС)
Легенда
В теории игр нередко применяют компьютерное моделирование, чтобы проанализировать поведение типовых стратегий в той или иной игре. Одной из распространённых форм представления моделируемой игры является платёжная матрица, где в зависимости от поведения каждого из игроков определяется изменение их счёта.
Промоделируем ситуацию, когда А и Б находят куст с ягодами и решают его поделить. Каждый из игроков может либо подождать, чтобы куст дозрел, либо собирает с него ягоды сразу. Пример платёжной матрицы для такой игры:
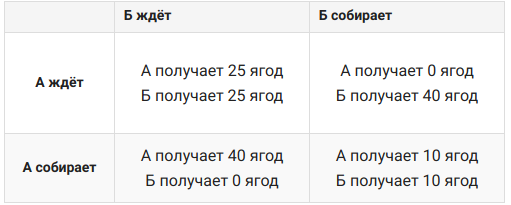
Пусть А и Б находят 10 разных кустов (т.е. игра моделируется 10 раундов подряд). Вы решили спросить знакомых, как бы они поступили в такой ситуации. Вам предложили следующие варианты (назовём их алгоритмами):
- «Кооператор» (код
К), который всегда соглашается подождать; - «Предатель» (код
П), который всегда собирает сразу; - «Око за око» (код
О), который сначала ждёт, а затем поступает так, как поступил соперник в прошлом раунде.
Так как все алгоритмы ведут себя строго детерминированно, вы можете посчитать результат каждого из турниров между ними. В этом и заключается задача.