Линейные блочные коды. Декодирование

Лебедев Валентин Павлович
кандидат физико-математических наук, старший научный сотрудник Института солнечно-земной физики СО РАН
Закодированный сигнал можно получить с помощью матрицы-генератора. Рассмотрим как декодировать сигнал, который прошел по каналу связи и был получен на входе декодера.
#ДекодированиеСигнала #БлочныеКоды #КодХемминга #КодГолея
На прошлом занятии мы разобрали проблему кодирования и увидели, что закодированный сигнал можно получить с помощью матрицы генератора. Мы разобрали пример этой матрицы для кода Хемминга (7, 4).
Пример был такой: на вход подавалась последовательность бит 1010 (назовём её K), далее она пропускалась через классический кодер, умножалась на матрицу генератора — G (как это делается смотрите в прошлой лекции). На выходе мы получили закодированное слово длиной 7 бит: 4 бита данных и 3 контрольных.
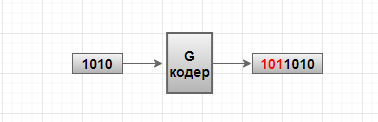
Рисунок 1
Далее эта посылка отправляется по каналу связи, в котором действуют шумы, помехи, и должна добраться до приемника.
Приемник регистрирует этот сигнал на какую-то антенну. Далее этот сигнал оцифровывается и отправляется на вход декодера, который должен из данной посылки вытащить наши информационные биты.
Представим наш кодер, далее сигнал подводится к передатчику и к антенне, которая излучает сигнал, в котором есть какие-то помехи, наводки. Сигнал проходит через этот канал связи, испытав на себе «прелести» шумов, поступает на приемную антенну. С приемной антенны через аналогово-цифровой преобразователь поступает в декодер.
Визуализируем наш сигнал: 1011010
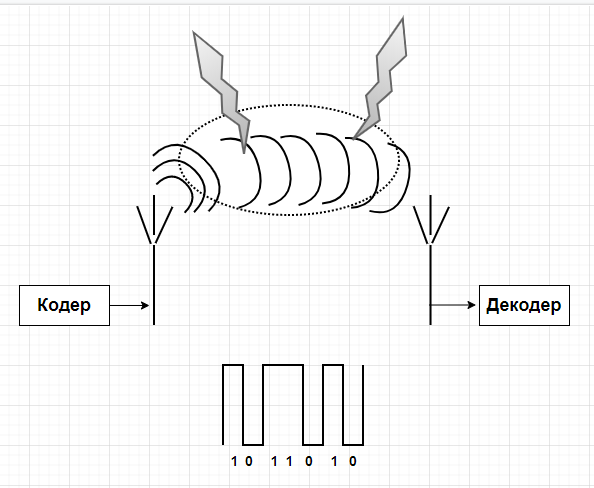
Рисунок 2
В этом сообщении есть какие-то наводки, шумы и т.д. Представим это случайной ломаной линией на рисунке 3.
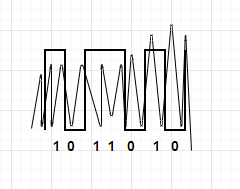
Рисунок 3
За счёт всплеска шумов в конце приёмник примет сигнал 1011011. То есть аналого-цифровой преобразователь (АЦП) понял, что на конце сообщения был сигнал, поэтому в этот бит записал 1, что, конечно же, является ошибкой.
Теперь посмотрим, как декодер может справиться с этой задачей. Фактически декодер должен решить обратную задачу относительно кодера. На вход декодера поступает n символов, он должен проверить есть ли ошибки, и если есть, то исправить их, и затем удалить контрольные биты — k. По аналогии с матрицей, которая кодирует, есть проверочная матрица, обозначается как H, она выглядит очень похоже на матрицу генератора, но отличается. Для кода Хэмминга (7, 4), который сейчас рассматриваем, эта проверочная матрица выглядит следующим образом:
Обратите внимание на блок из четырёх последних столбцов матрицы H, фактически он соответствует блоку из первых трёх столбцов генераторной матрицы G, который повёрнут на 90 градусов:
То есть можно написать проверочную матрицу H на основе генераторной (G).
Теперь попробуем умножить проверочную матрицу H на тот код, который получили, обозначим его CwR, где R — от слова “receive” принятый. Умножение производится по правилу: строка первой матрицы умножается посимвольно на столбец второй, после чего значения записываются в столбик и суммируются по модулю 2:
В результате сложения всех значений в каждой строке получается 3, по основанию 2 это равно единице, соответственно получаем матрицу из одного столбца и трёх строк, в каждой из которых стоит единица. Эта матрица называется синдромом.
Мы получили ненулевой синдром, следовательно в сообщение закралась ошибка.
А теперь в проверочной матрице H найдём столбец, который равен синдрому — это седьмой столбец. следовательно ошибка в седьмом бите!
Далее исправляем ошибку в сообщении 1011011 (ошибка в седьмом символе), следовательно правильное сообщение будет с противоположным значением в этом символе, то есть равно 0, а не 1, и итоговое исправленное сообщение будет 1011010.
Если теперь проверочную матрицу умножить на исправленное сообщение, то синдром будет равен нулю, а это значит, что ошибок нет. Если нет ошибок, то декодер знает, что последние четыре символа сообщения — это данные, а первые три — контрольные символы, и он оставляет только данные, а контрольные удалит.
Как видите, чтобы закодировать слово,
нужно исходное слово наложить на
матрицу-генератор, а там используется только сложение и умножение. Чтобы
декодировать сообщение, нужно проверочную
матрицу умножить на принятый сигнал,
определить синдром, если он ненулевой,
то по его виду найти ошибку и исправить, и тут тоже используется сложение и умножение по модулю 2, а это очень быстрая операция, поэтому кодер и декодер работают достаточно быстро.
Мы рассмотрели как устроены генерирующая матрица и проверочная на примере кода Хэмминга (7, 4), но подобные матрицы могут быть сгенерированы для любых блочных кодов, например для кода Хэмминга (15, 11), где 11 информационных и 4 проверочных, то есть в сумме блок состоит из 15 бит, и так далее.
Вообще говоря, так как коды Хэмминга исправляют однократную ошибку, а для того чтобы передать сигналы на далёкое расстояние, мы помним, что амплитуда сигнала падает с расстоянием, и поэтому шумы сильнее начинают влиять на сигнал, то могут возникнуть и неоднократные ошибки, но и больших кратностей. Для того чтобы избежать такие ошибки используют более сложные коды, например, код Голея. Он использовался для передачи данных с бортов Вояджер 1 и Вояджер 2, когда они пролетали с Юпитером и Сатурном. И там использовался код (23, 12), то есть 12 информационных бит, позволял исправлять трёхкратную ошибку, что существенно повышает надёжность кода.
Рисунок 4
На рисунке 4 вы можете увидеть матрицу-генератор для кода Голея (23, 12).
Рисунок 5
На рисунке 5 вы можете увидеть матрицу-генератор для расширенного кода Голея (24, 12). Сейчас он используется чаще, так как кратен восьми (24 бита — это 3 байта), и удобнее с ним работать.
Рисунок 6
А на рисунке 6 изображена проверочная матрица для кода Голея (24, 12), где чёрные кружочки соответствуют 1, а белые — 0.
В вашей работе, используя тот же аппарат, который рассмотрели для кода Хэмминга, вы можете использовать и для кода Голея, воспользовавшись этими матрицами. Попробуйте закодировать сигнал самостоятельно.
Так как код длины 12, то можно сгенерировать 4096 различных вариантов сообщений. А вариантов сообщений, которые можно получить, 224 — достаточно большой объём данных. Таблицу на 224 сейчас можно построить, так как существующие современные средства и компьютеры позволяют методом грубой силы определять нужный код. Есть конечно алгоритмы более умные, которые позволяют решать эту задачу быстрее, чем прямым перебором.
Следующее продвижение, связанное с помехоустойчивыми кодами, — это использование кодов Рида–Соломона, которые уже используют не бинарный алфавит (0 и 1), а на основе более богатых алфавитов. Эти коды являются блочным — кодируют отдельный блок целиком — но для того, чтобы разобраться как они работают, придётся достаточно глубоко копнуть в алгебру, то есть там достаточно алгебраический подход, когда создаётся некоторый генерирующий полином, который позволяет сформировать закодированное слово и соответственно декодировать. Эти коды обладают большей помехоустойчивостью, поскольку позволяют избавляться от многократных ошибок при относительно небольшой избыточности кодов. С ними можно будет познакомиться, когда вы поступите на первый–второй курс института и разберётесь с темой алгебраического подхода для генерации помехоустойчивого кода более подробно.
А вообще говоря, коды Рида–Соломона часто используются, когда записывается, например, на лазерный диск какая-то информация. Если посмотреть на многократно использованный диск, то можно легко увидеть множество царапин, иногда трещин, но тем не менее данные с него читаются. Это говорит о высокой надёжности этого кода, но и избыточность у него около 40%, и при этом он используется довольно часто. Разработчики программного обеспечения на Вояджерах сумели на лету перепрограммировать Вояджеры, и они передавали данные, используя код Рида–Соломона.
Для размышления
Пусть в рассмотренном сегодня примере при передаче сигнала 1011010 изменился не последний бит, а четвёртый, то есть принято было сообщение 1010010. Используя продемонстрированный подход, попробуйте её обнаружить.