Линейные блочные коды. Кодирование

Лебедев Валентин Павлович
кандидат физико-математических наук, старший научный сотрудник Института солнечно-земной физики СО РАН
Линейные коды достаточно распространены, их много разнообразных вариаций. Примером линейного блочного кода, который мы уже рассматривали, является код Хемминга.
#ТехнологииБеспроводнойСвязи #КодированиеСигнала #БлончныеКоды #КодХемминга
Продолжаем цикл занятий, посвященный темам технологий беспроводной связи. Сегодняшнее занятие посвящено такой актуальной теме, как линейные блочные коды, кодирование. Мы посмотрим, какие есть варианты, какие способы кодирования информации используются в работе.
Начнем с простых кодов. Простые коды ⏤
линейные блочные коды - некоторые
информационные сообщения разбиваются
на блоки, и каждый блок по-отдельности
кодируется, по-отдельности принимается
и декодируется. То есть каждый блок ⏤
некая независимая единица.
Примером линейного блочного кода, который мы уже рассматривали, является код Хемминга. Мы рассматривали, как он устроен на примере кода Хемминга (7,4) - где 7 бит ⏤ это длина блока, из них 4 бита ⏤ информационные, а 3 бита ⏤ контрольные.
Рассмотрим код Хемминга (n,k), где под n ⏤ общее количество бит в блоке и k ⏤ количество информационных бит в блоке.
Линейные коды достаточно распространены, их много разнообразных вариаций. Вы можете сами придумать какой-либо свой линейный блочный код и использовать его. Коды Хемминга в свое время были очень популярны ввиду простоты их реализации, что очень немаловажно, когда вы придумываете свой код, и, соответственно, они решают свою задачу. А именно, код Хемминга (7,4) исправляет однократную ошибку.
Давайте разберемся, почему он исправляет однократную ошибку?
Вернемся к коду Хемминга (n,k), где
-
k ⏤ количество информационных бит,
-
n ⏤ это общая длина блока,
-
r = n – k ⏤ это количество проверочных, или контрольных бит.
Таким образом, у нас k=4, 4 информационных бита.
Вообще говоря, Код Хемминга ⏤ двоичный
код, он работает на алфавите, алфавит в
нашем случае ⏤ это множество {0; 1}.
Поэтому количество возможных вариантов
так называемых входных слов 2k,
при k=4 количество возможных вариантов
входных слов будет 24 = 16.
Что делает кодер?
Поступает некоторый блок из k бит,
далее есть устройство или программа,
которая называется кодер. Она кодирует
ваше входное сообщение, то есть добавляет
в него некоторые дополнительные
проверочные символы. Фактически кодер
удлиняет сообщение на количество
проверочных символов r, и возвращает
некоторое закодированное слово длиной
уже n бит. Так работает любой кодер,
какой бы мы не смотрели, блочный он или
нет.
Таким образом, в случае кодирования
кода Хемминга (7,4) на входе есть таблица
шестнадцати вариантов: 0000, 0001, …, 1111, а
на выходе те же самые 16 вариантов, но
они снабжены еще проверочными символами.
Множество выходных слов отличается
друг от друга попарно всегда на 3
контрольных бита.
Рассмотрим пример. Пусть k=1, то есть вы хотите передать 1 бит, но так, чтобы при возникновении ошибки его можно было бы поправить. Сколько потребуется дополнительных бит, чтобы можно было восстановить сообщение?
Пусть отправляемый бит: 0.
Если вы предположите, что достаточно одного проверочного бита, значит, количество единичек должно быть четным, то есть вы добавляете в данном случае 0, тогда во время движения по каналу связи сообщение может исказиться:
00 ➞ 10 - четность изменилась (однократная ошибка)
01 - четность изменилась (однократная ошибка)
00 - в этом случае понимаем, что сообщение не исказилось
В случае с комбинациями (10 и 01) непонятно
какой символ был передан: 1 или 0? В данном
случае эти варианты равноправны, поэтому
одного проверочного символа никак не
хватает. Следовательно, нужно использовать
два проверочных символа.
И если вы передаете один бит данных (D) и у вас два контрольных бита (K1 и K2), то в зависимости от того, какой на входе бит, будут определяться контрольные символы.
D кодируется ➞ DK1K2
0 кодируется ➞ 000 ➞ при возникновении ошибки на выходе получим следующие варианты: 100, 010, 001.
Отсюда легко понять, что был передан именно 0.
Рассмотрим первый вариант — 100. Проверяем контрольные суммы.
D + K1 = 1 (mod 2) - значит, ошибка либо в первом (D), либо во втором бите (K1), далее приемник сравнивает данные и второй контрольный бит
D + K2 = 1 ( mod 2) - значит, ошибка либо в первом (D), либо в третьем бите (K2),
две ошибки в переданном сигнале быть не может, поэтому ошибка в данных.
Далее рассуждаем аналогично. Для сигнала 010:
D + K1 = 1 (mod 2) - значит, ошибка либо в первом бите (D), либо во втором бите (K1)
D + K2 = 0 (mod 2) - значит, ошибка именно в первом бите (D)
И продолжая рассуждение, мы можем определить, что ошибка в данном случае в во втором контрольном бите.
Те же самые рассуждения можно привести и для случая, если вы передаете три единички.
D кодируется ➞ DK1K2
1 кодируется ➞ 111 ➞ при возникновении ошибки на выходе получим следующие варианты: 011, 101, 110.
При передаче трех нулей в случае, когда в канале может быть ошибка, на выходе может прийти три различных варианта. При передаче трех единиц в случае, когда в канале может быть ошибка, на выходе тоже может прийти три различных варианта. И нужно помнить о том, что могут быть приняты сообщения без ошибок: 000, 111.
Всего два варианта на стороне передатчика, которые могут быть переданы, 111 и 000. А различных вариантов, которые могут быть приняты, с ошибками и без ошибок, восемь. При этом какой бы вариант вам не пришел, вы всегда можете определить, что конкретно было на стороне передатчика. Зная, как устроен кодер, программа кодера, которая таким образом закодировала сигнал, вы может разобраться, что было на входе, 0 или 1.
Обратите внимание, что мы обнаружили и
исправили однократную ошибку благодаря
тому, что исходные варианты, которые
сформировал кодер, отличаются именно
на три бита (000 и 111), если бы они отличались
на два бита, тогда было бы непонятно, с
какой стороны сигнала находится ошибка.
В данном примере расстояние Хемминга
будет равно 3. Под
расстоянием Хемминга подразумевается
количество бит, на которые отличаются
два сравниваемых числа.
Давайте попробуем разобраться, на какое количество бит наши кодовые комбинации должны отличаться, если мы хотим исправить двукратную ошибку.
Пусть,
-
квадратик — разрешенная комбинация, то есть та комбинация, которую выдает кодер,
-
крестик — комбинация, которая содержит в себе ошибки, то есть это те коды, которые наш кодер никак не мог выдать нам; это комбинации, которые появились в процессе приема, уже на стороне приемника.
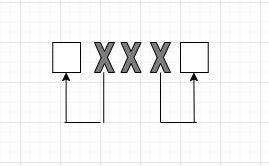
Итак, если принятый код имеет вид ◻ХХХ◻, то комбинации, которые содержат в себе ошибки - Х - говорят о том, что на самом деле были переданы ближние к ним разрешенные комбинации - ◻, была допущена однократная ошибка.
Если мы получили вариант, где стоит средний Х, это означает, что мы фиксируем ошибку, что такая комбинация не может быть, ее нет в перечне, и это двукратная ошибка.
Что привело к возникновению этой двукратной ошибки, откуда она, мы не знаем.
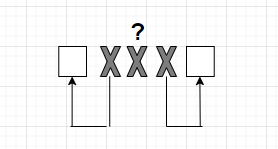
Мы можем только обнаружить ее, а исправить не можем.
Теперь возвращаясь
к вопросу: как исправить двукратную
ошибку?
Рассмотрим ситуацию, изображенную на рисунке.
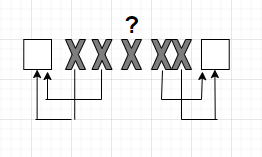
Принятый код имеет вид ◻ХХХХХ◻. Если мы принимаем эту комбинацию, то стрелками покажем с какими разрешенными комбинациями будут отождествляться комбинации с ошибками. Почему именно так? Потому что мы ищем ближайший разрешенный код. Но мы не знаем откуда произошла ошибка, которая находится в середине комбинации. Ошибка обнаружена, мы не можем её исправить. Таким образом, чтобы исправить двукратную ошибку, нужно, чтобы ближайшие кодовые слова отличались на минимум пять бит.
Такую схему рассуждения можно применить, если вы хотите сгенерировать код, который исправляет трехкратную или четырехкратную ошибку в вашем коде и так далее. Эти несложные рассуждения позволяют разобраться, сколько нужно проверочных символов, и как должны быть устроены слова, которые выдает кодер. Как слова должны отличаться друг от друга.
Мы поговорили про кодирование в случае,
когда мы хотим разработать код, который
исправляет однократную, двукратную,
трехкратную ошибку. Это так называемые
общие принципы. Возвратимся к нашему
коду Хемминга 7,4.
Код Хемминга 7,4 является совершенным кодом. Почему? Потому что все комбинации, которые возвращает ваш кодер, отличаются друг от друга ровно на 3 бита, то есть нет никакой избыточности, кодовое пространство заполняется максимально плотно. Количество комбинаций, которое может принять пользователь в случае, если вы работаете с кодом Хемминга 7,4, равно 27 = 128.
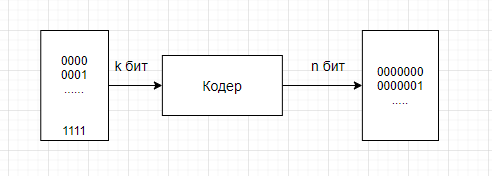
Поэтому, когда вы работаете с кодом
Хемминга 7,4, его можно использовать как
некоторый табличный код. Вообще говоря,
табличный код - это самый простой в
реализации код, когда вы четко ставите
в соответствии с входом - выход. Когда
вы декодируете, соответственно, тот
код, который вы приняли (принятый сигнал)
вы сравниваете с одним из 16 вариантов.
Там, где он ближе всего - где расстояние
по коду будет 1 или 0, будет сигнал,
который был на входе. Удалив контрольные
символы, получаете ту посылку, которую
передали.
В случае, когда вы кодируете 1 бит данных, то есть утраиваете ваш код, получается очень высокая избыточность. В этом случае можно использовать таблицы. То есть у вас будет таблица на стороне кодера и декодера, и кодер по номеру входного сигнала сразу возвращает выходной, при этом декодер действует также. Поэтому написать код Хемминга 7,4 можно, просто перечислив в массиве все возможные варианты.
На практике коды используются длинные.
Код должен спасать вас не только от
однократной ошибки, но и от многократной
ошибки (от двух-, трехкратной). Он должен
вас защищать, чтобы повысить надежность
канала связи. Поэтому используются коды
длиной 100, 200. А теперь представьте,
например, 2100 — это количество
вариантов, которые нужно закодировать
или найти, то есть это 1,267·1030
вариантов. Это, скажем, такой жесткий
вариант, когда вы простым перебором,
методом грубой силы декодируете сигнал?
Конечно, в современных устройствах так
не делают, то есть если в таком, простом
варианте это можно было сделать, то в
современных системах нет.
Для кодирования слов линейными блочными кодами используется генерирующая матрица или матрица-генератор. Это более простой подход, который позволяет кодировать намного быстрее.
Матрица-генератор как раз имеет размер (n*k), и в этом случае вам не надо хранить всю таблицу 2n, а достаточно всего n умножить на k чисел, что намного меньше. Теперь посмотрим, как устроен кодер, как устроена генерирующая таблица для кода 7,4. Посмотрим, как она работает. То, что мы рассмотрим, можно будет использовать на более длинные коды.
Генерирующая матрица обозначается буквой G, и для кода 7,4 она может быть построена на основе тех контрольных сумм, которые вы захотите сформулировать, то есть то, как сейчас она будет выглядеть, не означает, что это жесткий вариант, который мы будем использовать. Возможен другой вариант. Он может быть сформирован вами самостоятельно, в зависимости от того, на какие биты вы делаете ставку.
У нас 4 бита данных, поскольку мы рассматриваем код 7,4: d1 d2 d3 d4.
Контрольные суммы P1, P2, P3 устроим следующим образом:
P1 = d4 + d3 + d2 (mod 2)
P2 = d4 + d3 + d1 (mod 2)
P3 = d4 + d2 + d1 (mod 2)
Если формировать контрольные суммы иначе, например, вместо d4 поставить и от них все отписать, это нисколько не помешает нашей работе.
Матрица-генератор составляется следующим образом.
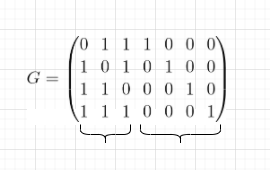
Первый столбец: смотрим на первую контрольную сумму, сюда не входил d1, поэтому на ее месте - 0, а входили d2, d3, d4, на их место ставим 1, 1, 1 соответственно. Второй столбец: во вторую контрольную сумму входил d1, поэтому на его месте - 1, не входил d2 — на его месте 0, d3, d4 — входит — 1, 1. Аналогично, строим третий столбец.
Следующая часть соответствует битам данных.
Теперь попробуем закодировать какое-то сообщение с помощью матрицы-генератора. Сообщение, которое мы хотим передать состоит из нескольких 1 и 0, это двоичные коды.
Сообщение: 1010. Мы хотим его передать.
Сообщение-слово будем обозначать w.
Кодовое слово, которое мы закодируем Cw = w * G
Обратите внимание w — строка, G — матрица
Поэлементно умножаем строку на столбец. В результате получим строку из 7 элементов. Первый элемент будет следующий: 1 × 0 + 0 × 1 + 1 × 1 + 0 × 1 (mod 2) = 1. Второй элемент: умножаем эту же строчку на следующий столбик и так далее.
Таким образом, в результате кодирования мы получили следующее:
(1010)→ G(кодер)→ (1011010).
Обратите внимание на следующий интересный момент: в последовательности 1011010 последние 4 символа - это наши данные, а первые 3 символа - это контрольные биты. И именно эта посылка уже уезжает дальше.
Для размышления
Закодируйте сообщение 1100 с помощью матрицы-генератора.
Материалы
- Сагалович Ю.Л. Введение в алгебраические коды (глава 4)
- Видео об Алгоритме кодирования и обнаружения ошибки кодом Хемминга
- Королев А.И. Коды и устройства помехоустойчивого кодирования информации. Мн.: 2002. - 286 с. (объёмный материал о кодировании за исключением глав 4 и 6)