Метод наименьших квадратов

Продолжаем разбирать задачи трека «Технологии беспроводной связи».

Вернемся к задаче определения углового ускорения вращения, которая у нас ставилась и решалась на стенде с шестеренками, на малом стенде. Обратите внимание, что сегодня рядом с малым стендом расположен его старший брат, большой стенд, на котором есть “радар”, “спутник”. “Спутник” может двигаться, “радар” его может отслеживать. Обратите внимание, что стенд с шестеренками может быть подключен через большой стенд.

На экране уже знакомая вам программа-интерфейс, которая теперь позволяет управлять как большим стендом, так и малым. Причем иконки в правом верхнем углу теперь все активны:

• сеть,

• “радар” (то есть управляющий компьютер обменивается данными с “радаром”),

• цветная картинка для “спутника” (есть общение между управляющим компьютером и бортовым компьютером “спутника”),

• иконка с шестеренками (управляющий компьютер может взаимодействовать с малым стендом).

Теперь посмотрим, как это можно проверить. Выбираем уже знакомую нам задачу - определения углового ускорения вращения шестеренок. Я запускаю наш стенд через управляющий компьютер и через большой стенд, и, как вы можете видеть, шестеренки начинают вращаться с ускорением, все быстрее, быстрее и быстрее. Шестеренки - те же самые, что мы и рассматривали раньше. Сейчас они вращаются, соответственно, мы помним, что инфракрасный сигнал модулируется. Мы убедились, что вся система может функционировать и работать как единое целое. Дальше этот модулированный сигнал с каждой шестеренки можно передать на спутник, дальше со спутника передать его на радар, и тут уже могут возникать различные варианты задач.

В 2018 году на Олимпиаде, которая проходила в Иннополисе, была примерно такая постановка задачи: есть некоторый макет “спутника” на Земле, на котором мы можем проверять, как он будет отрабатывать ту или иную ситуацию, так называемое “пугало”, и есть реальный “спутник”, на который мы уже заливаем программы, которые, в свою очередь, проверили на нашем “пугале”. Данные мы получили.

Я напомню условие задачи про ускорение, оно было следующим:

С данного макета дан сигнал при равномерном вращении шестеренок и при равноускоренном. По этим данным нужно было определить угловое ускорение вращение каждой шестеренки.

Мы увидели, что сигнал в случае, если шестеренки вращаются равномерно, выглядит периодическим образом.

Рисунок 1. Равномерное вращение шестеренок

Периодичность хорошо подчеркивает наша автокорреляционная функция: мы видим четкие пики для каждой шестеренки. Напоминаю: красный сигнал - это большая шестерня, синий - средняя, и зеленый - малая шестеренка. Естественно, чем меньше радиус шестеренки, тем она вращается быстрее. Это мы видим по пикам нашей автокорреляционной функции. Значит, в случае, если у нас есть сигнал с равномерным вращением, мы можем оценить отношение периодов на каждой шестеренке, и, следовательно, мы можем оценить отношение угловых ускорений на этих шестеренках тоже.

Теперь посмотрим, как выглядит сигнал в случае, когда наши шестеренки вращаются равноускоренно.

Рисунок 2. Равноускоренное вращение шестеренок

Как мы видим, периодичности уже никакой нет, у всех автокорреляционных функций есть только главный пик, а дальше нет ничего такого интересного, это и понятно, потому что, соответственно, интервал обращения шестеренки вокруг своей оси каждый раз уменьшается, то есть он в точности сам себя не повторяет.

Заметим интересный момент: малая шестеренка моделирует сигнал не только узором на своей рубашке, но и зубчиками, а происходит это вследствие того, что наш свет и фотодиод - не точечные, то есть они излучают сигнал, который проходит как и через непосредственно окна на шестеренке, так и через межзубчатое пространство. Логично в этом смысле было зацепиться за самый быстрый периодический элемент - сигналы зубчиков для того, чтобы оценить угловое ускорение. На рисунке мы видим интересную “расчесочку”. Есть узор, связанный с узором на шестеренке с окнами и стенками, а мелкая вариативность связана как раз с модуляцией сигнала нашими зубчиками.

Далее логично определить положение каждого зубчика. Например, мы определяем максимальный уровень сигнала, сбрасываем данные в отдельный файл, и дальше начинаем работать с этими данными.

Давайте посмотрим, как выглядят наши данные, построенные на одном графике.

Рисунок 3. Угловая скорость

Что приведено на этом графике на рисунке 3? По оси оси абсцисс Х, приведен конкретный момент времени, а по оси ординат Y, приведена разность между двумя соседними максимумами в том сигнале, который мы разбираем.

Давайте обратимся к следующему графику сигналов и их автокорреляционных функций, чтобы было понятно, о чем идет речь.

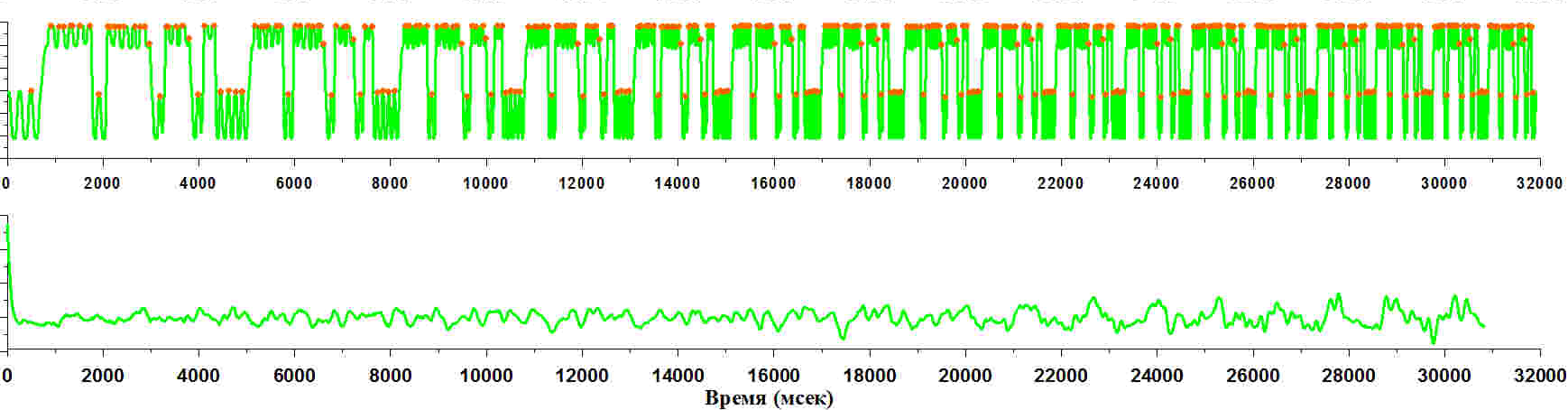
Рисунок 4 (сигнал, образованный маленькой шестеренкой)

Обратите внимание на пики, связанные с прохождением каждого конкретного зуба шестеренки через фотодиод. Мы определяем положение вот этих максимумов. А дальше мы построим разницу по времени между двумя соседними максимумами. Эта разница по времени соответствует одной двадцать пятой (1/25) периода.

Почему 1/25? Потому что зубчиков на шестеренке здесь всего 25. А если здесь всего 25 зубчиков, то соответственно этот интервал времени соответствует 1/25 периода. И так как угловое расстояние между зубчиками невелико, то мы можем считать, что за время поворота от зубчика до зубчика угловым ускорением можно пренебречь. Значит, можем считать, что на этом интервале времени шестеренка вращалась с постоянной угловой скоростью, практически с постоянной.

Таким образом, на графике на рисунке 3 мы с вами видим картину, как раз этих интервалов времени. Фактически, это интервал времени, но только приведенный к углу поворота, и крестиками на этом рисунке обозначены измеренные времена между соседними максимумами. Вы видите, что в целом картина напоминает некоторый линейный тренд, он обозначен зеленой линией. Но если внимательно присмотреться, то можно проследить и некоторый вторичный тренд, внизу графика на рисунке 3. Фактически мы наблюдаем здесь два интересных процесса. Сегодня мы разберемся, с чем эти процессы связаны.

Прежде, чем к этому переходить, давайте посмотрим, каким образом мы вписали в черные крестики прямую линию. Это диктуется условием задачи, что движение равноускоренное. А что значит равноускоренное движение? Это значит, что у вас угловая скорость вращения линейно растет со временем. Зависимость скорости углового вращения от времени выглядит следующим образом:

ω = ω₀ + β * τ

τ — время,

β — ускорение углового вращения, β = const,

ω — скорость углового вращения,

ω₀ — скорость углового вращения при старте.

Мы видим, что в какой-то нулевой момент времени при τ = 0, угловая скорость была равна нулю. Дальше она начинает линейно расти от τ, β — это ускорение углового вращения, это, как раз, наша константа.

Фактически мы видим, что нам нужно определить уравнение прямой, в котором, две неизвестных:

• угловая скорость при старте ω₀,

• ускорение углового вращения β.

Для решения таких задач, когда у нас есть такое облако точек, и в них надо вписать прямую линию, как правило, используется так называемый “метод наименьших квадратов”. Что же это за метод, как он работает?

Обратите внимание, что на графике на рисунке 3 есть некоторые крестики, которые пунктирной синей линией соединены с зеленой, с искомой линией. Это так называемая “невязка” - расстояние между конкретным и теоретическим измерениями.

При этом крестик - это конкретное измерение, теоретическое - наша теоретическая функция (зеленая прямая). И в методе наименьших квадратов, сумма квадратов этих невязок, от каждого крестика до зеленой линии, должна быть минимальна. Вот поэтому этот метод и называется - метод наименьших квадратов.

Сумма невязок от измерений до нашей некоторой теоретической линии должна быть минимальна, сумма квадратов должна быть минимальна. Представим это утверждение в виде некоторого математического выражения.

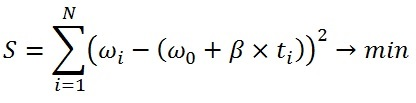
Обратите внимание, что здесь:

S — это сумма невязок,
ω_i – (ω₀ + β × t_i) — невязка, 
ω_i — это та угловая скорость, то значение, которое мы получили в измерениях, крестики на графике на рисунке 3,
ω₀ + β × t_i — уравнение прямой, в которое входят те параметры, которые нужно определить, а именно:
ω₀ — это начальная угловая скорость, 
β — ускорение углового вращения, β = const,
t_i — это i-ый интервал времени, в котором было получено i-ое измерение i.

То есть фактически мы видим разницу между измеренным значением и тем значением, которое должно быть. 

Итак, в нашем выражении вы видите два неизвестных параметра, и их нужно определить. Причем, функция в этих точках, при каком-то ω₀, при какой-то β, должна быть минимальна. Таким образом, если мы возьмем производные по этим параметрам, то в точке минимума производные должны обращаться в ноль.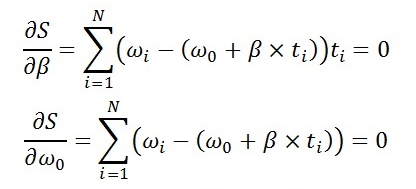

Фактически, мы получаем два выражения, которые приводят нас к системе двух уравнений, которые уже можно решить, пользуясь методами школьной математики.

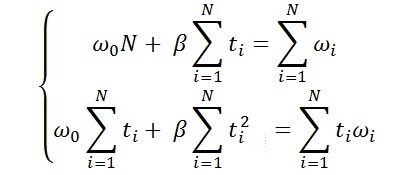
Еще раз, что в этой системе уравнений нам известно, а что неизвестно? Итак, нам, конечно же, неизвестно то, что мы хотим найти, это ω₀ и β, у нас две неизвестных, поэтому два уравнения.

Ну а что нам известно?

N — это количество точек, это количество черных крестиков на графике 3,
t_i — это время, в которое был получен каждый черный крестик,
ω_i, сумма ω_i — это как раз те текущие угловые скорости, которые мы измерили с помощью такой разницы, как интервал времени между двумя соседними максимумами.

Разрешить эту систему из двух уравнений с двумя неизвестными несложно. Предлагаю конечные выражения сделать самостоятельно.

Именно таким образом, решая данную систему уравнений, и была получена зеленая линия на графике на рисунке 3. И вроде бы хорошо, зеленая линия действительно совпадает с тем трендом, который у нас есть. Но в глаза бросаются крестики, которые тоже каким-то образом ложатся на некоторый тренд. Понятно, что в нашем сигнале, который мы таким образом анализируем по соседним пикам, присутствует как-будто бы еще какой-то процесс. Зеленая линия, в-основном, выражает процесс, который мы исследуем, данной точности уже хватает для того, чтобы решить задачу, имею ввиду, удовлетворить тем требованиям, которые были заявлены во время постановки задачи.

Второй интересный тренд четко бросается в глаза. Что это такое? Какие-то точки лежат практически на прямой. Интересно выяснить, с чем это может быть связано. Кроме того, если мы убедимся, что эти точки действительно связаны с каким-то другим процессом, то в определении динамики изменения угловой скорости эти точки можно отбросить, и тогда уже они не будут влиять на наши результаты по определению самого тренда, который мы хотим определить.

Фактически, мы подозреваем, что это есть некоторый мешающий сигнал, который нам хотелось бы отбросить и точнее определить наклон этой прямой. Давайте подумаем, с чем это может быть связано? Когда возникает такая задача, какими процессами определяется такой характерный разброс облака измеренных черных точек. В общем-то, одним из действенных методов является метод пристального вглядывания в данные, которые вы получили. Давайте попробуем это сделать.

Сейчас попробуем под микроскопом, что называется, разглядеть, как выглядят те максимумы, которые мы определили. Мы определили их с помощью обычных алгоритмов определения максимума в массиве. Давайте посмотрим на рисунок, где приведен фрагмент, маленькая часть сигнала, которая связана с зубцами.

Рисунок 4. Срез сигнала

На рисунке 4 видно характерное изменение сигнала, связанное с узором на шестерне. “Пальцы” на рисунке 4 связаны с нашими зубчиками на шестерне.

После пристального вглядывания, когда мы все анализируем, можно увидеть, что натворил стандартный алгоритм поиска максимума.

Он поставил точки (выделены оранжевым) - это положение максимума, на краю зубца, прямо две точки рядышком, дальше, точка стоит не посередине зубца, а привязана где-то приближенно к краю, и дальше почему-то наши точки привязаны то к одному краю импульса, то к другому. А когда у нас есть четкий острый максимум, тут все в порядке. Эти точки не совсем корректно себя ведут, не совсем корректно определяется наш максимум. Давайте подумаем, что это такое?

Надо помнить, что у нас живая система, аналоговая, и поэтому здесь любые небольшие неточности в положении зуба, что-то еще, могут играть свою роль. Поэтому посмотрим следующий момент. Почему же у нас вот такой плоский срез (рисунок 4): сигнал растет, а потом резко фиксируется в некоторый максимум, потом проходит какое-то время, он достигает опять некоторого уровня и опять начинает себя вести нормально.

Давайте попробуем выяснить, как будет выглядеть наш сигнал, который будет модулироваться только зубчиками шестеренки. Обратите внимание, что мы сейчас для демонстрации подготовили шестеренку такого же размера, как наша маленькая шестеренка, но уже без узора. Сейчас мы ее поставим, запустим стенд еще раз и посмотрим, как будет выглядеть сигнал в случае, если у нас узора здесь не будет. И давайте попробуем запустить наш стенд с тем же самым ускорением и интервалом работы. В принципе, этого можно было легко достичь, не меняя шестеренку. Каким образом? Если, например, какой-то черной изолентой залепить щели на шестеренке. Но для чистоты эксперимента просто взяли и предложили нашему стенду отработать со сплошной шестеренкой. Давайте посмотрим, как будет выглядеть сигнал уже в этом случае.

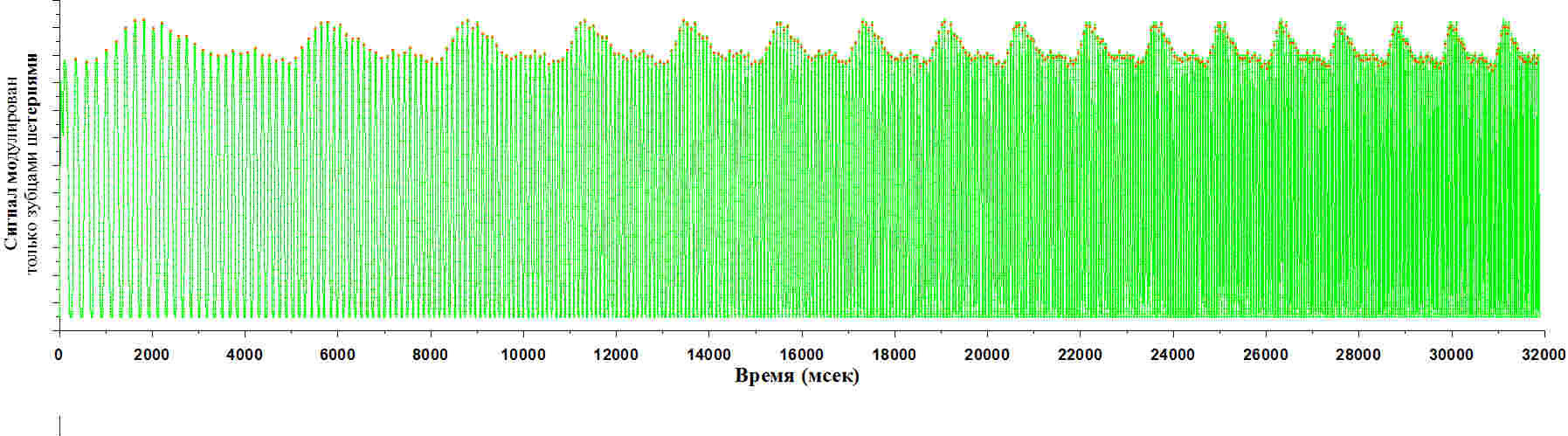
Рисунок 5. Сигнал модулирован только зубцами шестерни

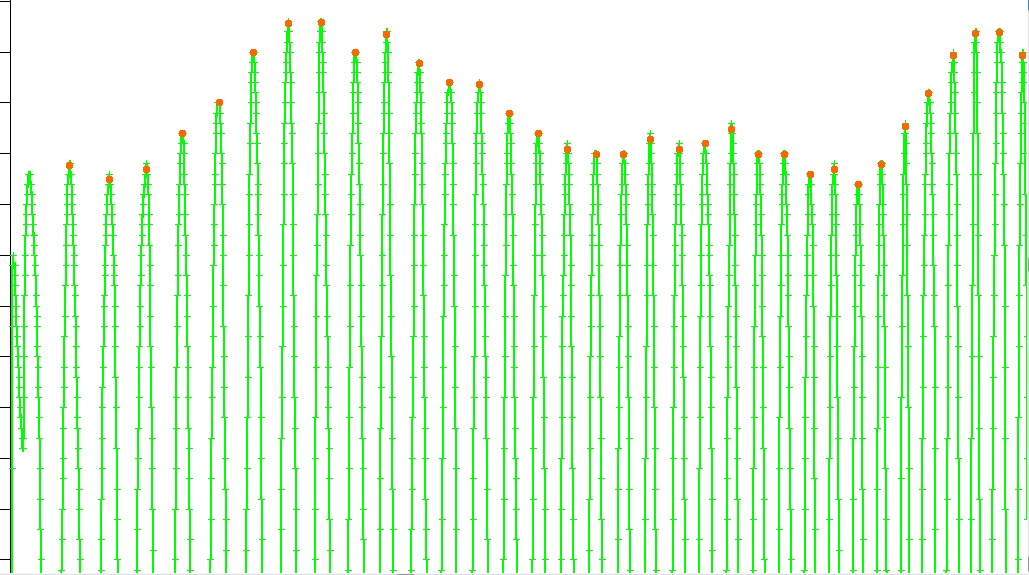
Рисунок 6. Сигнал модулирован только зубцами шестерни, крупным планом

На графике на рисунке 5 представлена динамика сигнала, связанная как раз только с зубчиками. Здесь четко видна периодичность, а плавное повышение и понижение сигнала связано с неидеальностью шестеренки. Стенд настолько чувствителен, что он может зарегистрировать даже эту небольшую неидеальность шестеренки. Важно, что в этом случае пики - четкие, выраженные, и поэтому не составляет никакого труда определить максимум в этом сигнале. Четкие точки на каждом максимуме можно найти самыми простыми школьными способами определения максимума в массиве.

После того, как мы определили максимумы, построим график того, как меняется интервал времени между соседними максимумами в зависимости от времени.

Рисунок 7. Угловая скорость

На графике на рисунке 7 тот же интервал времени работы, примерно 32 секунды. Черными точками показан интервал времени между соседними максимумами, который нам уже известен. Зная количество зубцов, мы можем рассчитать угловую скорость.

Обратите внимание, что теперь четко видно один тренд. Черные точки, в основном, все ложатся на один тренд. Но со временем, когда шестеренки уже набирают высокую скорость, невязка между зеленой линией и черными точками становится все шире. Это связано с тем, что интервал времени становится все меньше, поэтому, если есть какие-то неточности в определении максимума, они в этом случае для нас все чувствительнее. Но самое главное для нас здесь, что не появляется никакого дополнительного трека. Если за эти пики отвечают только зубчики шестеренки, то все аккуратно ложится на линейный тренд, и наклон этой зеленой линии определяет угловое ускорение. Можно сказать, что мы идеально определили то угловое ускорение, которое было задано в задаче. Неточность составляет меньше 0,1 °/c².

Итак, в случае если у нас работают только зубчики, нет никаких дополнительных трендов, четкий сигнал, все хорошо.

Теперь вернем нашу шестеренку с прорезями. Но теперь попробуем сделать так, чтобы каким-то образом убрать сигнал от зубчиков, то есть оставим сигнал от окошек и стенок, а от сигнала от зубчиков попробуем избавиться - скрыть его.

Возвращаю шестеренку на прежнее место, заменяем тестовый блок заменяем на тот, с которым мы работали. Что мы сделаем? Мы закроем часть светодиода и фотодиода, которые у нас расположены напротив зубчиков, оставим только ту часть приемника, которая регистрирует сигнал напротив щелей, и будем снимать сигнал только с узора. Итак, запускаем стенд, опять то же самое угловое ускорение вращения, все те же самые параметры, но теперь наши зубчики нам мешать не будут.

Фактически мы приходим к пониманию, что у нас есть два типа сигналов. Первый тип сигнала связан с зубчиками, второй тип сигнала связан с узорами на шестеренке, эти два сигнала в данном случае аддитивно складываются. Итак, если мы посмотрим теперь на сигнал, то мы увидим следующую динамику.

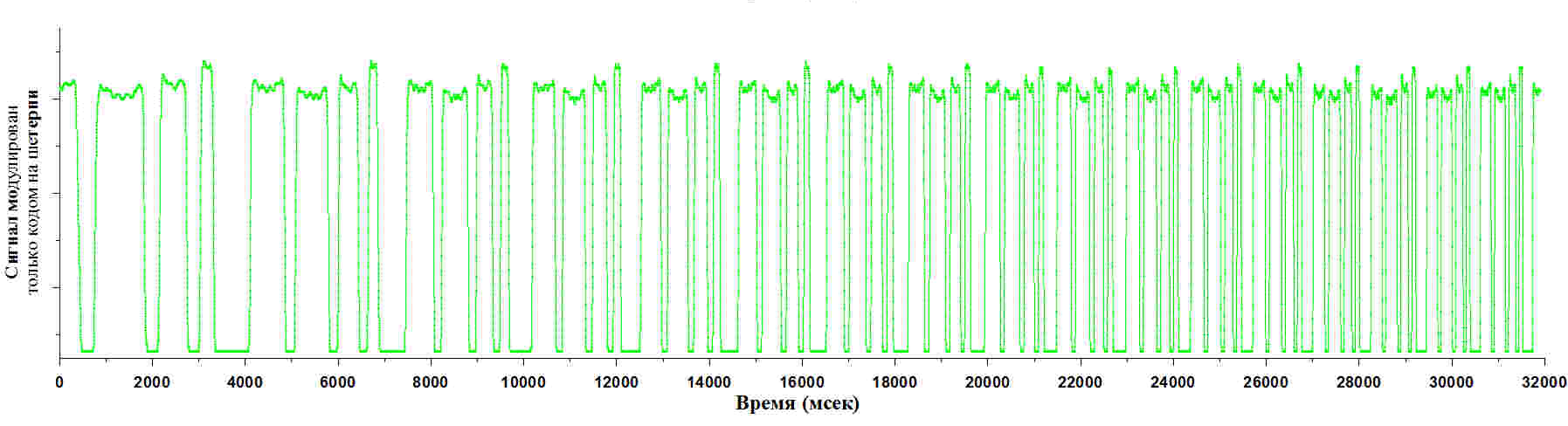
Рисунок 8. Сигнал модулирован только кодом на шестерни

Обратите внимание, что в сигнале осталась только динамика, связанная с узором на шестеренке. На графике рисунка 8 виден характерный код. Верхушка каждого импульса изрезанная, на краях, по переднему и по заднему фронту каждой такой верхушки видны пики.

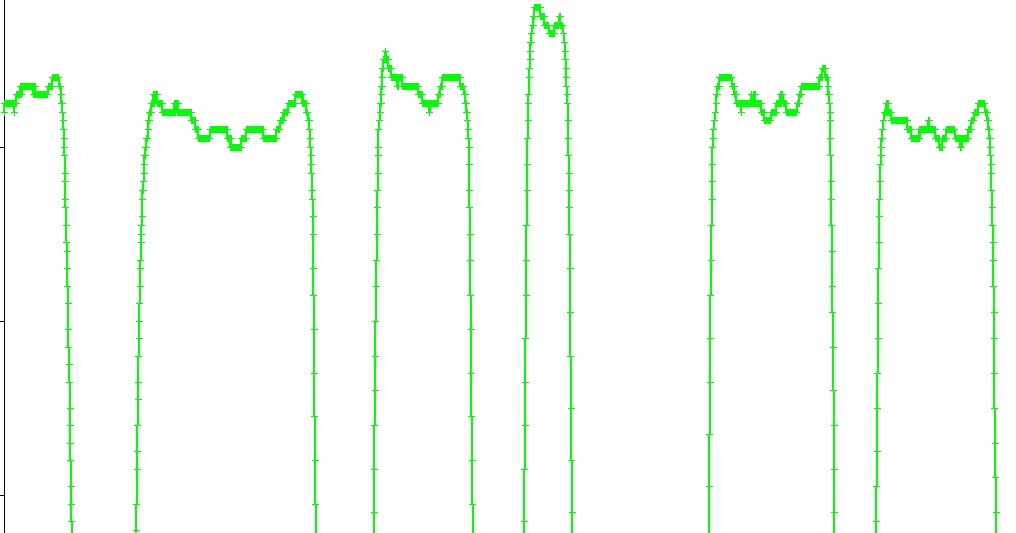
Рисунок 9. Сигнал модулирован только кодом на шестерне, крупным планом

Вспомним, где наш алгоритм определил пики? Как раз на переднем и на заднем фронте, как правило, он за них хватается. Когда мы убираем крупную динамику, связанную с зубчиками шестеренки, четко видно два пика по краям изрезанных верхушек, иногда бывает и где-то в серединке проскочит.

Таким образом, суммарный сигнал опять представляет собой то же самое, что и прежде.

Рисунок 10. Суммарный сигнал

Давайте теперь внимательно проанализируем два наших сигнала. Обратите внимание, что если мы работали только с одними зубчиками (график на рисунке 5), все равно синусоида нигде не обрезалась, все очень четко и плавно. А в случае, когда мы суммируем два сигнала (график на рисунке 10), у нас появляется обрезка по определенному уровню. Это связано с тем, что наступает момент, когда сигнал превышает что называется “динамический диапазон”. Это означает, что, несмотря на то, что открытая площадь фотодиода становится больше, но, начиная с какого-то времени, сигнал перестает расти. И этот момент - это так называемый наш “динамический предел”. У любого физического устройства есть такой предел, с каким бы устройством мы не работали, начиная с какого-то уровня, сигнал уже не регистрируется. Сейчас мы с этим столкнулись.

Обратите внимание, что в сигнале (график на рисунке 10) виден некоторый уровень отсечки, поэтому простыми способами максимумы определяются не совсем хорошо. Мы не будем выдумывать каких-то изощренных вещей, чтобы можно было решить эту проблему. Давайте попробуем разобраться, с чем был связан дополнительный тренд при анализе максимума у суммарного сигнала, когда мы лучше понимаем как выглядит наш сигнал, мы видим, что это сумма двух сигналов. Если внимательно посмотреть на этот сигнал, а на сигнал всегда надо смотреть внимательно, когда вы его исследуете, то вы можете заметить следующий интересный факт.

Рисунок 11. Потеря пика

На рисунке 11 приведена динамика суммарного сигнала, где у вас открыты и окошки и зубчики работают. Обратите внимание на интересный момент, который выделен черным овалом. Определились максимумы слева и справа от этого овала. Если присмотреться, то можно увидеть, что расстояние между этими двумя максимумами больше, чем между двумя соседними пиками, как правило. Это связано с тем, что здесь наложилось два процесса.

Первый процесс ⎼ это резкий фронт возрастающий, связан с наползанием окошка, то есть момент, когда фотодиод стал открываться, но в этот же момент на границе оконного фронта, где окошечко начинается, появляется зубчик, который закрывает, опять-таки, свою часть, то есть окошечко открывается, а зубчик закрывает, и поэтому этот зубчик у нас спрятался на фоне этого окна. И если внимательно посмотреть, то мы увидим здесь точку перегиба, как-будто бы зубчик хотел сформироваться, но не успел, окошко открылось раньше, и так далее. И мы видим, что эти точки должны повторяться, вот они у нас повторяются, потому что шестеренка же проворачивается, они повторяются, и мы их видим дальше. И период между ними уменьшается.

Так что мы с вами разобрались, с чем был связан дополнительный тренд, давайте вернемся к этой исходному графику на рисунке 3. Мы разобрались, что дополнительный тренд связан с тем, что пики на некоторых зубчиках не определились из-за того, что борются два процесса, зубчик закрывает ⎼ окошко открывается, и окошко, конечно, больше, чем зубчик, оно побеждает. Остается избавиться от этого дополнительного процесса.

Когда вы работаете с методом наименьших квадратов, вы предполагаете, что шум у вас что называется “нормальный” - Гауссов шум. Об этом мы говорили на лекции, когда говорили про шумы, про корреляционные функции, про сигналы. Так вот, когда вы говорите про метод наименьших квадратов, вы предполагаете, что шум нормальный, симметричный и распределен как Гауссова функция. Причем, среднее должно быть нулевым, то есть он должен быть не смещен, в среднем несмещенным.

Давайте попробуем проанализировать этот шум. Фактически с чем связаны эти отклонения? Они связаны с тем, что присутствует шум в сигнале. Давайте попробуем построить наш шум, посмотрим на него более подробно.

Рисунок 12. Разница между измеренной угловой скоростью и определенной с помощью МНК

На графике рисунка 12 с левой стороны из данных вычтен линейный тренд, эта зеленая линия из черных крестиков убрана, то есть фактически мы видим, что точки теперь ориентированы горизонтально, и присутствует дополнительный тренд, мы тоже его видим, он никуда не делся, он остался.

А теперь построим гистограмму распределения отклонения, вот этих невязок. Она приведена на правом рисунке. Обратите внимание, что в среднем, после вычитания, максимум приходится где-то на ноль, то есть все точки, в-основном, группируются около нуля, но здесь также в левой части нашей гистограммы появился дополнительный пик, связанный с этими точками. Ну а Гауссов шум, нормальный шум, он определяется характерным разбросом, и фактически это ширина основного пика.

Давайте теперь оставим только те точки, которые соответствуют этой ширине, а всё, что не попадает в эту основную гистограмму, мы уберем, и посмотрим, как будут выглядеть наши данные в этом случае.

Рисунок 13

Итак, если выполнить все эти операции, определить характерную ширину этого основного распределения и оставить только те точки, которые в него попадают, мы получим уже следующий сигнал (график 9). После того, как мы отбросили точки, которые в наши ворота не попадают, то черные точки не покрашены. То есть те точки, которые попадают в наши ворота, выделены оранжевым, а те, которые не попали, так и остались черными. И теперь будем работать только с оранжевыми точками. Попробуем уже в них вписать прямую линию. На графике 9 она отмечена оранжевой пунктирной линией.

Обратите внимание, что она теперь идет круче и очень точно совпадает с правильным ответом, намного точнее, чем зеленая. То есть, если зеленая - это точность 1 °/c², то здесь - примерно 0,25 °/c².

А теперь проанализируем распределение тех точек, которые остались после селектирования.

Рисунок 14. Облако точек, которые остались после селектирования, и распределение этих точек

На графике слева на рисунке 14 мы видими облако точек, которые остались после селектирования, и распределение этих точек, которое представлено красной гистограммой справа на рисунке 14. Распределение очень точно напоминает Гауссов шум, черной линией в эти данные вписана по методу наименьших квадратов как раз Гауссова кривая, которая описывает характеристику нашего шума. То есть шум, как правило, маленький, в основном эти точки сгруппированы около нуля, но есть и точки, которые дальше от нуля, но их меньше. И в общем-то распределение достаточно хорошо напоминает Гауссову функцию.

Для того, чтобы получить ответ как можно точнее, мы с вами сделали дополнительную операцию, даже две операции. Первая операция, или нулевая, это операция, когда мы пристально смотрим на данные. Вы получаете некоторое облако точек и начинаете их анализировать, начинаете с ними разбираться, пытаетесь в них увидеть какой-то тренд, какую-то зависимость. И когда вы их внимательно посмотрите, изучите, вам ваша интуиция, ваши знания подскажут, как действовать в вашем каждом конкретном случае.

Для размышления

Попробуйте построить график зависимости угловой скорости от времени по функции ω=ω₀+β*τ. Подберите параметры ω₀ и β на ваше усмотрение, а время для простоты вычислений от 0 до 10 с с шагом в 1 с. Затем вручную нанесите несколько точек выше или ниже расчётных, как «измеренные». После чего подсчитайте сумму невязок и посмотрите, как она будет меняться, если убирать различные “измеренные” точки.

Материалы

• Полное математическое описание метода наименьших квадратов с примерами и доказательством