Видео-теория: Теория вероятностей

 

Тема этого занятия Теория вероятностей.

Что такое теория вероятностей и зачем она нужна?

Мы живем в непредсказуемом мире. Мы не знаем, какая погода будет завтра — у нас есть лишь прогноз, который говорит о вероятности, но не дает стопроцентной гарантии. Бросая монету, мы знаем, что выпадет орёл или решка, но не можем точно предсказать, какая именно сторона. Вытаскивая карту из колоды, мы можем лишь оценить шансы на появление нужной масти или достоинства. Теория вероятностей — это раздел математики, который позволяет численно измерять эту непредсказуемость и работать с ней.

Она помогает отвечать на практические вопросы. Например, представим незавершённую игру, где сделаны ставки, а победитель забирает всё. Внезапно игру невозможно продолжить (пропал кубик). Как справедливо разделить выигрыш? Отдать всё игроку с преимуществом — нечестно, ведь его соперник еще имел шанс отыграться. Поделить поровну — тоже несправедливо к тому, кто был близок к победе. Теория вероятностей помогает решить эту задачу, рассчитав шансы каждого игрока на победу в момент остановки игры.

Вероятность — это числовая мера возможности наступления некоторого события.

Как измерить вероятность?

Существует несколько подходов к измерению вероятности:

1. Классический подход (симметрия). Если все исходы события равновероятны (например, при броске «честного» кубика), то вероятность каждого исхода равна 1/n, где n — общее число исходов.

2. Статистический подход (частота). Вероятность оценивается на основе данных из прошлого. Если за последние 1000 бросков кубика шестёрка выпала 100 раз, мы можем предположить, что вероятность её выпадения близка к 100/1000 = 0,1.

3. Субъективный подход (экспертное мнение). Когда невозможно провести эксперимент или исходы несимметричны, вероятность оценивается на основе мнения эксперта. Например, эксперт считает, что вероятность запуска нового проекта — 0,9, а дилетант — 0,1.

События, которые происходят со 100% вероятностью, называются достоверными, их вероятность равна 1. Сумма вероятностей всех возможных исходов всегда равна 1 (или 100%).

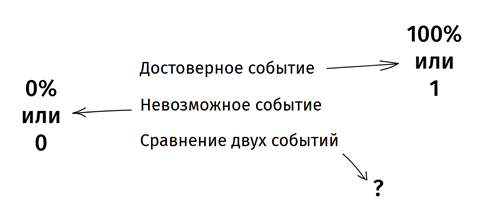
Переходим к подсчету вероятности и алгебре событий.

Что такое вообще алгебра?

Это когда у нас есть некоторое количество объектов, и мы с ними производим операции, то есть складываем, вычитаем и получаем какой-то новый объект, если в двух словах, то в алгебре событий вероятность выражается операторами ИЛИ, И, НЕ.

ИЛИ — это когда мы объединяем 2 события и смотрим, чтобы либо то, либо иное событие произошло.

И — это когда мы смотрим пересечения этих событий и то и то должно произойти одновременно.

НЕ — это когда мы инвертируем событие, то есть предполагаем, что это событие не произойдёт то есть, отрицаем событие.

Допустим, ручка должна упасть со стола и чай НЕ должен быть пролит.

Множество всех событий вычисляется по этим трём операциям.

Для элементарных событий или несовместимых взаимоисключающих событиях допустим у нас есть один кубик у него шесть граней, и мы можем посчитать и составить такую вероятность выпадения единицы и тройки. Если мы скажем, что нам нужно чтобы выпало 1 или 3, то мы складываем события и считаем вероятность. Если же мы говорим, что одновременно должны выпасть те же 1 и 3 то это невозможное события и вероятность равна нулю, потому что такого не может произойти. чтобы на одном кубике при одном броске выпали и 1 и 3.

p(А или B) = p(A) + p(B)

p(А и B) = p(∅) = 0

Для независимых событий считается следующим образом, допустим у нас уже появилось два кубика, и мы должны посчитать вероятность выпадения каких-то определённых чисел на том и на другом кубике, то есть объединяем и также складываем эти вероятности, а для того, чтобы вычислить что и то и то событие произойдет мы уже посчитаем эти вероятности.

p(А или B) = p(A) + p(B)

p(А и B) = p(A) × p(B)

Для зависимых же событий мы поступаем следующим образом, если мы представим круги Эйлера и посмотрим на их пересечение, то мы считаем одну вероятность одного событий, и вероятность второго события. Мы должны вычесть их пересечение, то есть звено по середине, иначе она почитается дважды и вероятность будет недостоверна.

p(А или B) = p(A) + p(B) – p(А и B)

p(А и B) = p(А) × p(B)

Основная теория для задач теории вероятности в прошлом выражалась в том, что если у каждого элементарного события есть какая-то ценность, то нам необходимо вычислить ценность ещё непроизошедшего события, то есть нужно было рассчитать с какой вероятностью произойдёт что-то в будущем и прийти к тому, что нам необходимо вычислить математическое ожидание случайной величины.

Математическое ожидание рассчитывается по сумме произведений получения вероятности на число этой вероятности.

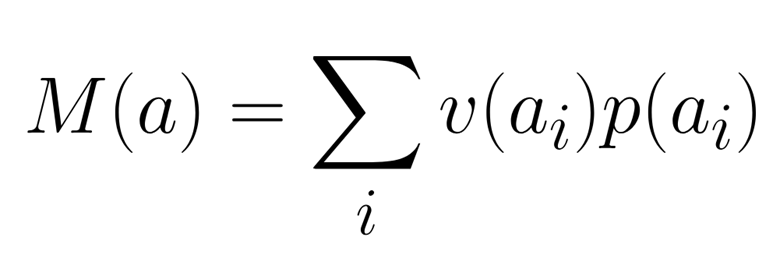
Примеры задач

Пример 1. Если на двух кубиках выпадет 11 или больше, мы проиграем миллион. Если нет — то выиграем два! Ставки сделаны, каков ожидаемый выигрыш?

То есть, мы можем посчитают что 11 у нас выпадет если на кубиках будет 5 и 6, 6 и 5, 6 и 6. То есть всего 3 комбинации из 36 возможных или 1/12. Вероятность того, что мы выиграем 2 миллиона, будет составлять 11/12. Достаточно хороший шанс.

Пример 2. Надо ли брать зонт, если вероятность дождя 20%?

Если вероятность дождя двадцать процентов существуют следующие исходы:

1.        Взяли зонт, пошел дождь.

2.        Взяли зонт, не пошел дождь.

3.        Не взяли зонт, пошел дождь.

4.        Не взяли зонт, не пошел дождь.

 Во всех этих вариантах разная выгода, допустим дождь не пошел, и мы взяли зонт, значит мы зря с собой тащили этот зонт, такая ситуация не очень приятна. Или, наоборот, мы его не взяли, но попали под дождь и промокли, тоже неприятно.

Пример 3. На отрезок длины 1 бросим случайную точку. Какова вероятность того, что мы попадём в участок до 0,3 до 0,7?

мы рисуем всю линию и выделяем наш интересующей отрезок и вычисляем что в этом отрезке получается четыре части.

И таких задач бывает очень большое и большое множество, с ними вы познакомитесь как на практике, так и сами на математике.