Видео-теория: Математические модели

Сегодня мы поговорим о такой интересной теме, как математические модели. Рассмотрим, что такое модель, что такое математическая модель и зачем нам вообще об этом знать.

Когда мы говорим о математических моделях, в первую очередь стоит поговорить о самой математике. Выводы, которые дает математика, никак не зависят от нашего мнения, желаний и предпринятых действий. Знания в области математики зависят только от наших усилий и способности вычислять, но при этом сама математика объективна и едина для всех. Например, если Вася и Петя будут что-то вычислять по одной и той же теореме Пифагора, они придут к одному и тому же результату, при условии, что правильно выполнят все расчеты.

Теперь поговорим о реальности. В отличие от математики, наше знание о реальности никогда не может быть полным. Возьмем, к примеру, десятирублевую монету. Мы можем вычислить ее примерный вес, а взяв партию монет, — средний вес. Мы можем примерно представить, из каких металлов она состоит. Если мы посмотрим на нее в микроскоп, то увидим целый мир, недоступный обычному глазу: окислы, глубокие царапины. Но мы никогда точно не узнаем, сколько у этой монеты было владельцев, сколько раз ее подкидывали или из какой конкретно руды она была произведена. Реальность, в отличие от нашего мнения о ней, зависит от наших действий, но наше знание о ней всегда будет неполным и основанным на опыте.

Итак, у нас есть две концепции:

1. Математика — общая для всех, доступная, а знания в ней основаны на труде и вычислениях.

2. Реальность — тоже общая, но наши знания о ней неполны и основаны на опыте.

Как же их связать? Для этого и существуют математические модели.

Что такое математическая модель?

Математическая модель — это когда мы берём фрагмент реальности и описываем его с помощью математического языка: формул, уравнений, алгоритмов. Это позволяет нам работать с этим фрагментом в математической структуре, где всё легко посчитать и проанализировать.

Например, рассмотрим взаимодействие Земли и Луны. Мы не можем экспериментировать с этими гигантскими системами: двигать их или менять скорость вращения. Это либо привело бы к катастрофе, либо нам просто не хватило бы ресурсов. Но мы можем создать математическую модель их движения и точно рассчитать, в какое время и на каком расстоянии Луна пролетит мимо Земли с определённой скоростью. Такой эксперимент невозможен в реальности, но математика позволяет нам получить точный ответ.

Модель строится следующим образом: мы берём какую-то систему (назовем ее Система №1). Она большая, сложная, труднодоступная, у нее слишком много свойств и нюансов. Чтобы ее изучить, мы создаем Систему №2 — небольшую, простую, удобную для исследования и понятную нам. Она должна быть похожа на большую, но никогда не сможет полностью ее заменить. В этом случае Система №2 является моделью Системы №1.

Хороший пример — исследования в медицине. Человек — это сложнейшая система (Система №1). У каждого индивида своя реакция на события и медикаменты. Мы не можем проводить опыты, например, по тестированию новых лекарств, сразу на людях. Поэтому для этой задачи мы берём лабораторную мышь — это наша Система №2. Мышь живёт недолго, быстро размножается, и мы можем отслеживать реакцию на препарат через поколения. А что связывает человека и мышку? То, что их базовые реакции на многие медикаменты похожи.

Важно понимать, что универсальных моделей не бывает. Модель всегда создается для решения конкретной задачи и с учетом ограничений — ресурсов, времени, бюджета. У любой модели есть автор, который закладывает в нее нужные ему свойства и определяет ее назначение. Именно поэтому на один и тот же процесс разные авторы могут создать совершенно разные модели.

Инструменты математического моделирования

Для работы с данными в моделях используются различные методы. Рассмотрим два из них:

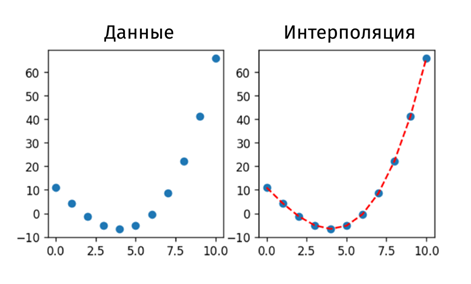
• Интерполяция — это способ найти недостающие данные внутри известного диапазона. Представьте, что человек завтракал овсянкой каждый день, кроме среды, данные за которую отсутствуют. Используя интерполяцию, мы можем с высокой вероятностью предположить, что в среду он тоже ел овсянку.

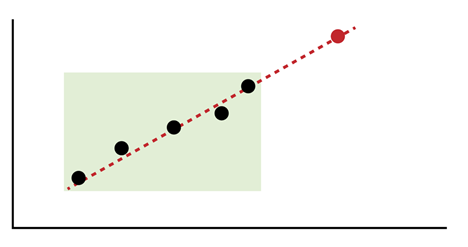
• Экстраполяция — это прогнозирование будущих значений на основе имеющихся данных. Если мы знаем, что человек ел овсянку семь дней подряд, мы можем экстраполировать этот паттерн и предположить, что он будет есть ее и на следующей неделе. Однако экстраполяция не всегда работает точно и лучше всего подходит для анализа больших объемов данных.

Разнообразие математических моделей огромно, но нас прежде всего интересуют те, которые можно перевести в компьютерную программу, где все вычисления за нас будет выполнять машина.

Структура нашей работы выглядит так:

1. Берём интересный нам фрагмент реальности.

2. Переводим его в математическую модель.

3. Переводим модель в программный код.

На каждом этапе могут возникнуть проблемы. Модель может оказаться неудачной. Программа может содержать ошибки. Если и модель, и код некорректны, то и результаты будут неверными.

Но что же происходит на стенде ИЭС?

Мы рассматриваем энергетику, но мы не можем рассмотреть эту сферу на примере мирового опыта, ввиду сложности структуры, и мы рассматриваем энергетику с точки зрения обеспечения энергии какого-то конкретного посёлка, тогда энергосистема этого посёлка будет представлена на энергостенде.

Реальных потребителей мы заменим на потребителей, которые разделим по классу, напоминаю, что есть три класса потребителей: жилые дома, больницы и заводы. У разных потребителей есть разные классы потребностей и, в целом, обеспечение энергией у них происходит по-разному. В реальности есть альтернативная энергетика, на стенде же она представлена с помощью генераторов солнечной и ветряной энергии, а для того, чтобы они работали, нам необходимо симулировать погоду, ведь ветряная электростанция окажется бесполезной, если не будет ветра, а солнечная станция будет бесполезной, если у нас никак не будет светить солнце или мы не будем как-то симулировать работу солнца.

Человеко-машинные взаимодействия мы можем заменить на скрипты и экспертные системы команд. Инфраструктурная задача решается еще проще, то есть в реальности мы строим какой-то посёлок и обеспечиваем его энергией, а на стенде ещё проще. На этапе «Аукцион» разыгрываются потребители (дома, заводы больницы) и это, в совокупности, является нашим посёлком, то есть мы решаем сложную задачу стенда в условиях стеснённых во времени. Прикручиваем к стенду разделение на команды и соперничество между ними и все это превращается в командное соревнование.

Мы можем подвести итог, что энергосистема представляет из себя модель, которая реализуется скриптами и экспертными системами каждой команды.